%@metapost:nordsep2000.mp
%@Titre: Nord (Sept.) -- 2000
\textbf{Les trois parties sont indépendantes.}
\begin{center}
\textbf{\Large{Partie I}}
\end{center}
\par\compo{2}{nordsep2000}{1}{
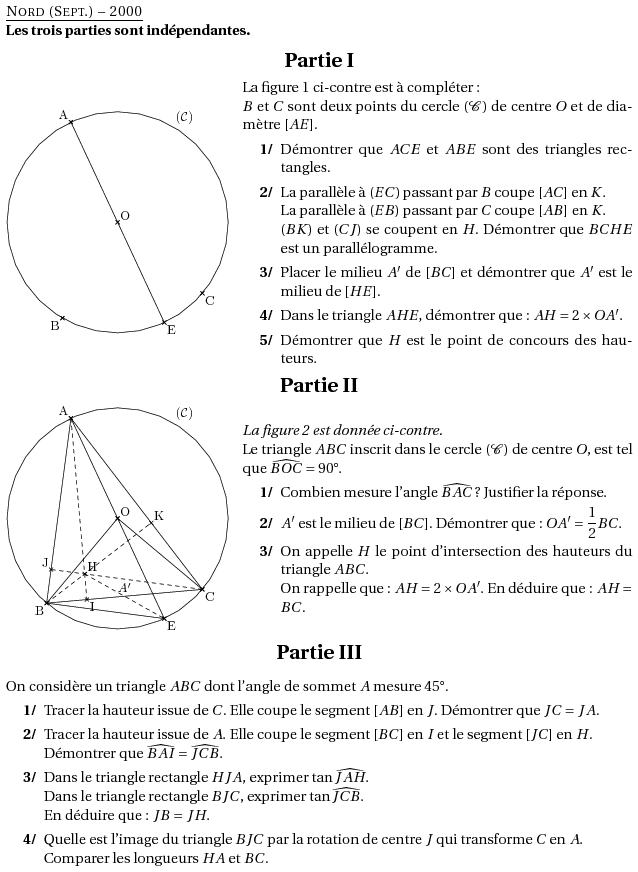
La figure 1 ci-contre est à compléter :

$B$ et $C$ sont deux points du cercle $\cal{(C)}$ de centre $O$ et de diamètre $[AE]$.
\begin{myenumerate}
\item Démontrer que $ACE$ et $ABE$ sont des triangles rectangles.
\item La parallèle à $(EC)$ passant par $B$ coupe $[AC]$ en $K$.
\\La parallèle à $(EB)$ passant par $C$ coupe $[AB]$ en $K$.
\\$(BK)$ et $(CJ)$ se coupent en $H$. Démontrer que $BCHE$ est un parallélogramme.
\item Placer le milieu $A'$ de $[BC]$ et démontrer que $A'$ est le milieu de $[HE]$.
\item Dans le triangle $AHE$, démontrer que : $AH=2 \times OA'$.
\item Démontrer que $H$ est le point de concours des hauteurs.
\end{myenumerate} 
}
\begin{center}
\textbf{\Large{Partie II}} 
\end{center}
\par\compo{3}{nordsep2000}{1}{
\textit{La figure 2 est donnée ci-contre.}
\\Le triangle $ABC$ inscrit dans le cercle $\cal{(C)}$ de centre $O$, est tel que $\widehat{BOC}=90$\degres.
\begin{myenumerate}
\item Combien mesure l'angle $\widehat{BAC}$ ? Justifier la réponse.
\item $A'$ est le milieu de $[BC]$. Démontrer que : $OA'=\dfrac12BC$.
\item On appelle $H$ le point d'intersection des hauteurs du triangle $ABC$.
\\On rappelle que : $AH=2 \times OA'$. En déduire que : $AH=BC$.
\end{myenumerate}
}
\begin{center}
\textbf{\Large{Partie III}}
\end{center}
On considère un triangle $ABC$ dont l'angle de sommet $A$ mesure 45\degres.
\begin{myenumerate}
\item Tracer la hauteur issue de $C$. Elle coupe le segment $[AB]$ en $J$. Démontrer que $JC=JA$.
\item Tracer la hauteur issue de $A$. Elle coupe le segment $[BC]$ en $I$ et le segment $[JC]$ en $H$.
\\Démontrer que $\widehat{BAI}=\widehat{JCB}$.
\item Dans le triangle rectangle $HJA$, exprimer $\tan \widehat{JAH}$.
\\Dans le triangle rectangle $BJC$, exprimer $\tan \widehat{JCB}$.
\\En déduire que : $JB=JH$.
\item Quelle est l'image du triangle $BJC$ par la rotation de centre $J$ qui transforme $C$ en $A$.
\\Comparer les longueurs $HA$ et $BC$.
\end{myenumerate}