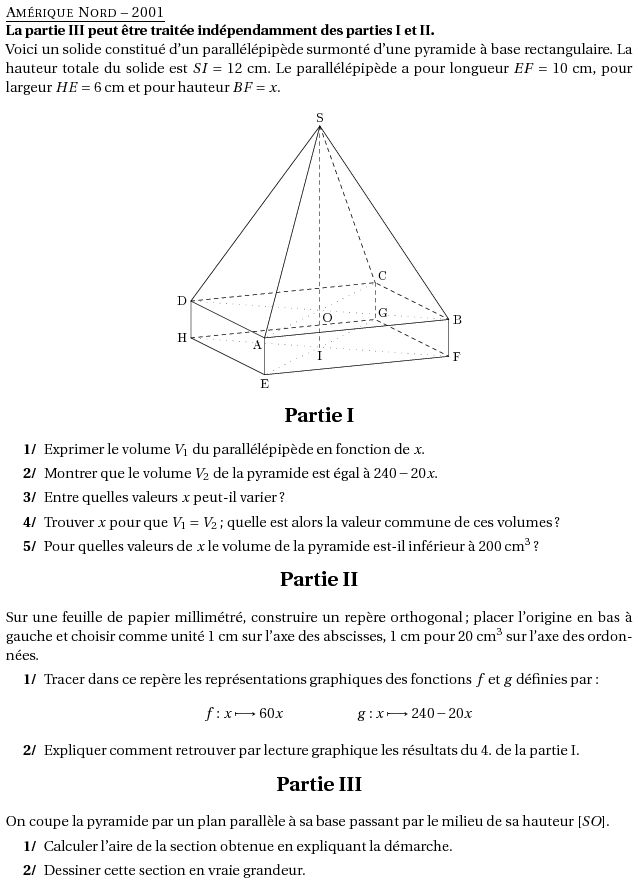
%@metapost:ameriquenord2001.mp %@Titre: Amérique Nord -- 2001 \par\textbf{La partie III peut être traitée indépendamment des parties I et II.} Voici un solide constitué d'un parallélépipède surmonté d'une pyramide à base rectangulaire. La hauteur totale du solide est $SI=12$~cm. Le parallélépipède a pour longueur $EF=10$~cm, pour largeur $HE=6$~cm et pour hauteur $BF=x$. $$\includegraphics{ameriquenord2001.2}$$ \begin{center} \textbf{\Large{Partie I}} \end{center} \begin{myenumerate} \item Exprimer le volume $V_1$ du parallélépipède en fonction de $x$. \item Montrer que le volume $V_2$ de la pyramide est égal à $240-20x$. \item Entre quelles valeurs $x$ peut-il varier ? \item Trouver $x$ pour que $V_1=V_2$ ; quelle est alors la valeur commune de ces volumes ? \item Pour quelles valeurs de $x$ le volume de la pyramide est-il inférieur à 200~cm$^3$ ? \end{myenumerate} \begin{center} \textbf{\Large{Partie II}} \end{center} Sur une feuille de papier millimétré, construire un repère orthogonal ; placer l'origine en bas à gauche et choisir comme unité 1~cm sur l'axe des abscisses, 1~cm pour 20~cm$^3$ sur l'axe des ordonnées. \begin{myenumerate} \item Tracer dans ce repère les représentations graphiques des fonctions $f$ et $g$ définies par : \[f : x \longmapsto 60x\kern2cm g : x \longmapsto 240-20x\] \item Expliquer comment retrouver par lecture graphique les résultats du 4. de la partie I. \end{myenumerate} \begin{center} \textbf{\Large{Partie III}} \end{center} On coupe la pyramide par un plan parallèle à sa base passant par le milieu de sa hauteur $[SO]$. \begin{myenumerate} \item Calculer l'aire de la section obtenue en expliquant la démarche. \item Dessiner cette section en vraie grandeur. \end{myenumerate}