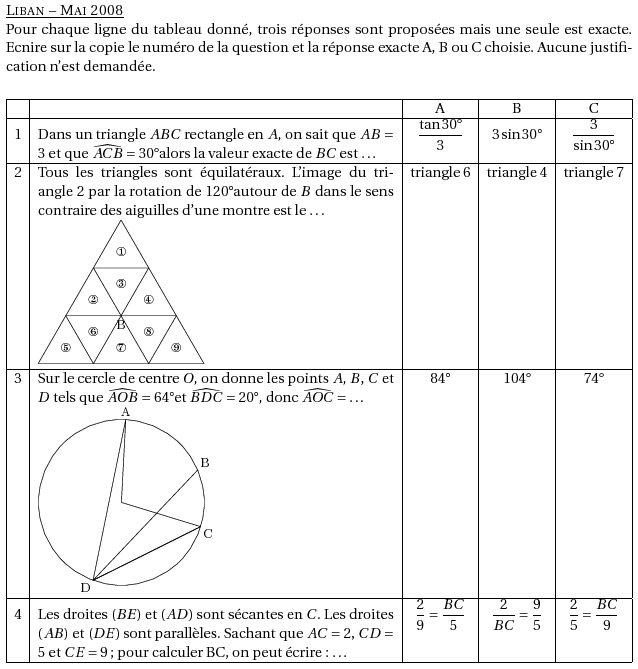
%@metapost:BLiban2008.mp %@Titre:Liban -- Mai 2008 Pour chaque ligne du tableau donné, trois réponses sont proposées mais une seule est exacte. Ecnire sur la copie le numéro de la question et la réponse exacte A, B ou C choisie. Aucune justification n'est demandée.\\ \medskip \begin{tabularx}{\linewidth}{|c|X|c|c|c|} \hline && A& B&C\\ \hline 1&Dans un triangle $ABC$ rectangle en $A$, on sait que $AB=3$ et que $\widehat{ACB}=30$\degres alors la valeur exacte de $BC$ est \ldots&$\dfrac{\tan 30\degres}3$&$3 \sin 30\degres$& $\dfrac3{\sin 30\degres}$\\ \hline 2&Tous les triangles sont équilatéraux. L'image du triangle 2 par la rotation de 120\degres autour de $B$ dans le sens contraire des aiguilles d'une montre est le~\ldots \par\includegraphics{BLiban2008.1} &triangle 6&triangle 4&triangle 7\\ \hline 3&Sur le cercle de centre $O$, on donne les points $A$, $B$, $C$ et $D$ tels que $\widehat{AOB}=64$\degres et $\widehat{BDC}=20$\degres, donc $\widehat{AOC}=\ldots$ \par\includegraphics{BLiban2008.2}&84\degres&104\degres&74\degres\\ \hline 4&Les droites $(BE)$ et $(AD)$ sont sécantes en $C$. Les droites $(AB)$ et $(DE)$ sont parallèles. Sachant que $AC=2$, $CD=5$ et $CE=9$; pour calculer BC, on peut écrire : \ldots&$\dfrac29=\dfrac{BC}5$ &$\dfrac2{BC}=\dfrac95$ &$\dfrac25=\dfrac{BC}9$\\ \hline \end{tabularx}