Plans perpendiculaires

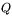
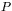
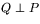
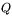
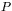
Définition 4   Un plan $Q$ est perpendiculaire à un plan $P$ ($Q \perp P$), si il existe une droite de $Q$ orthogonale à $P$. (Dans ce cas on a aussi $P \perp Q$).

Remarques :

• l'exemple qu'il faut avoir en tête est celui d'un cube : deux faces quelconques non parallèles sont perpendiculaires.

• Si $P \perp Q$ alors toute droite de l'un n'est pas orthogonale à l'autre, c'est vrai pour l'une d'entre elles.( Dans un cube $ABCDEFGH$ les faces $ABFE$ et $ABCD$ sont perpendiculaires mais la droite $(AF)$ n'est pas orthogonale à la face $ABCD$ car elle n'est pas orthogonale à (AB))

• Si $P \perp Q$ et $P' \perp Q$ alors $P$ et $P'$ ne sont pas nécessairement parallèles (facile à voir dans un cube avec les faces). Cette relation de perpendicularité de plans est donc moins souple que celle de perpendicularité de droites.

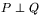
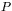
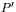
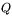
Théorème 12   Si $P$ et $P'$, deux plans sécants, sont perpendiculaires à un même plan $Q$, alors leur intersection est orthogonale à $Q$.

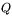
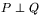
Théorème 13   Si $P \perp Q$, toute droite de l'un, qui est orthogonale à leur intersection, est orthogonale à l'autre. (voir la figure de la définition précédente)