Calculer un calendrier avec LATEX,
le dessiner en 3D avec PSTricks
Manuel Luque
24 avril 2 003
1 Objectifs, outils et méthodes adoptés
1.1 Objectifs
Il s’agissait de calculer avec LATEX, un calendrier valable de l’an 2 000 à l’an 2 099 (je suis optimiste),
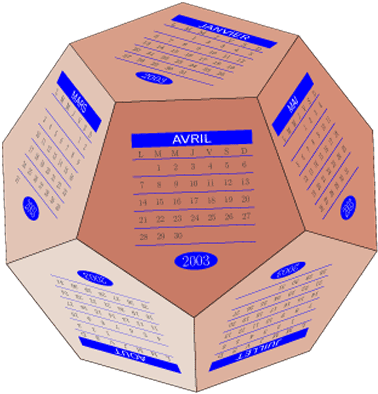
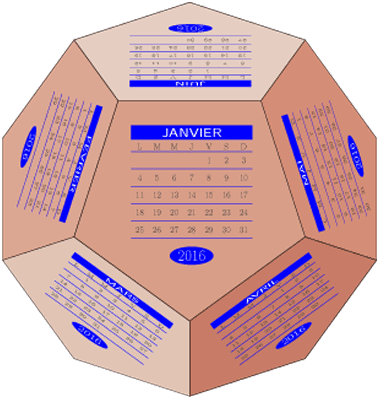
puis d’adopter une méthode originale de représentation en 3D, en plaçant chaque mois sur l’une des faces d’un
dodécaèdre. Un calendrier de ce type était, il y quelques années, offert par les visiteurs médicaux des laboratoires
PFIZER.
1.2 Outils adoptés
Il existe déjà un calendrier écrit en LATEX, dont les calculs sont faits directement en
TEX. Il s’agit de calendar, écrit par Michael Barret et disponible sur le serveur du CTAN ; c’est très bien
fait.
Un calendrier en 3D, dessiné avec PSTricks, est déjà proposé depuis plusieurs d’années par Denis Girou sur :
http://tug.org/applications/PSTricks/More (lien invalide).
Donc, rien de neuf, mais revu à ma façon : pour ma part j’ai décidé d’utiliser les macros du package fp de Michael
Mehlich, qui forment un excellent outil de calcul. La lecture du code écrit avec ce package est plus compréhensible que
celui écrit en TEX de base.
Pour la représentation en 3d, j’ai aussi, utilisé PSTricks de Timothy Van Zandt, et en particulier l’extension
pst-3d.
1.3 Méthode adoptée
La méthode de calcul des jours de semaine du calendrier est déduite de quelques observations
:
- Le 1 janvier 2 000 est un samedi. On adopte la convention de représenter les jours de semaine par un numéro : j’ai
choisi :
| lundi | mardi | mercredi | jeudi | vendredi | samedi | dimanche |
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
- Une année ordinaire comprend 365 jours, or 365 = 52 × 7 + 1. Il y a donc un décalage de 1 jour dans le nom des
jours pour l’année suivante si elle est ordinaire elle aussi. Autrement dit le 1 janvier 2 001 devrait être un dimanche
(6 + 1 = 7). Or l’an 2 000 est bissextile et comporte 366 jours : le décalage sera de 2, le 1 janvier 2 001 correspondra
au numéro 6 + 2 = 8 = 1 (modulo 7).
- Sur la période retenue 2 000/2 099 les années divisibles par 4 : 2 000, 2 004, 2 008 etc. sont bissextiles. On
déterminera donc si l’année choisie est bissextile en testant si elle est un multiple de 4.
% test d’une année bissextile
\FPeval{\YearBissextil}{(\psk@CalendrierA)/4}
\FPtrunc{\YearBissextil}{\YearBissextil}{0}
\FPeval{\YearBissextil}{(\YearBissextil)*4}
\FPtrunc{\YearBissextil}{\YearBissextil}{0}
\ifnum\YearBissextil=\psk@CalendrierA
etc.
|
- Pour une année choisie, on calculera le décalage par rapport à 2 000, en comptant les années et en
ajoutant 1 chaque fois qu’il y aura dans cet intervalle une année bissextile (en tenant compte de
2 000).
- On retient pour le début de chaque mois :
| mois | année ordinaire | année bissextile |
|
|
|
| janvier | 1 | 1 |
| février | 32 | 32 |
| mars | 60 | 61 |
| avril | 91 | 92 |
| mai | 121 | 122 |
| juin | 152 | 153 |
| juillet | 182 | 183 |
| août | 213 | 214 |
| septembre | 244 | 245 |
| octobre | 274 | 275 |
| novembre | 305 | 306 |
| décembre | 335 | 336 |
| |
2 L’utilisation
2.1 Utilisation simple
Si on veut voir uniquement le mois de l’année choisie, on fera, par exemple
:
\Calendrier[An=2099,Mois=12]
|
Cette étude ne teste pas si les valeurs introduites pour l’année(An) et le mois(Mois), sont correctes
!
Par défaut, la commande \Calendrier affiche le mois et l’année en cours.
2.2 Le calendrier en 3D
La commande s’écrit très simplement :
pour avoir le calendrier de l’année en cours. Si le schéma est trop grand à votre goût, encadrez la commande par un
\scalebox{0.5}{\dodecaedre}
Pour avoir le mois d’avril face à soi, on écrira, par exemple :
\scalebox{0.5}{\dodecaedre[Vx=-\rd,Vy=-\rc,Vz=0,viewangle=160]}
|
Vx, Vy, Vz sont les valeurs des paramètres de viewpoint=-5.85 -3.62 0 de la commande \ThreeDput de pst-3d, qui
sont les coordonnées d’un vecteur définissant la direction où se trouve l’observateur (la direction de la projection
parallèle).
On jouera aussi sur le paramètre viewangle, pour amener la face observée dans le bon sens de la
lecture.
Pour avoir le mois de janvier face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=-\rc,Vy=0,Vz=-\rd,An=2016,viewangle=108]}
|
Pour avoir le mois de février face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=\rc,Vy=0,Vz=-\rd,An=2016,viewangle=180]}
|
Pour avoir le mois de mars face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=0,Vy=-\ra,Vz=-\rb,An=2016,viewangle=144]}
|
Pour avoir le mois de mai face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=-\rd,Vy=\rc,Vz=0,An=2016,viewangle=198]}
|
Pour avoir le mois de juin face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=0,Vy=\ra,Vz=-\rb,An=2016,viewangle=216]}
|
Pour avoir le mois de juillet face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=-\rc,Vy=0,Vz=\rd,An=2016]}
|
Pour avoir le mois d’août face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=0,Vy=-\ra,Vz=\rb,An=2016,viewangle=-36]}
|
Pour avoir le mois de septembre face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=\rd,Vy=-\rc,Vz=0,An=2016,viewangle=-18]}
|
Pour avoir le mois d’octobre face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=\rd,Vy=\rc,Vz=0,An=2016,viewangle=18]}
|
Pour avoir le mois de novembre face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=0,Vy=\ra,Vz=\rb,An=2016,viewangle=36]}
|
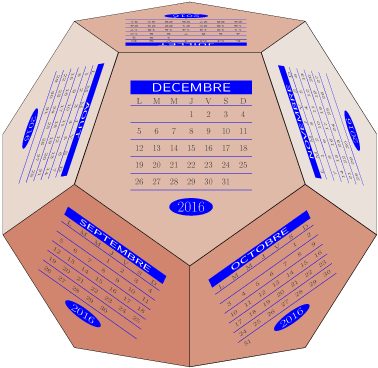
Pour avoir le mois de décembre face à soi, on écrira :
\scalebox{0.5}{\dodecaedre[Vx=\rc,Vy=0,Vz=\rb,An=2016]}
|
3 Que reste-t-l à faire ?
- Placer les jours fériés.
- Dessiner automatiquement le mois en cours, face à notre regard.
- Débusquer les erreurs, si vous en trouvez. . .
- Les sources : documentation et sources du calendrier3D