
|
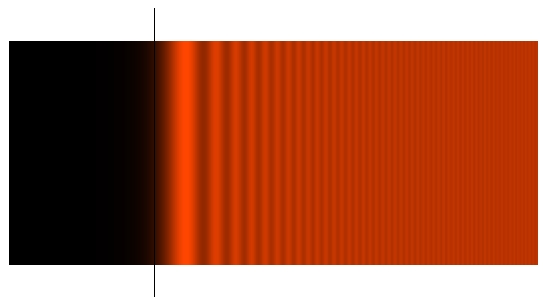
| Figure 2 : diffraction par un bord d'écran rectiligne, obtenue en lumière rouge. Le trait noir représente la limite de l'ombre géométrique. |
1. Avant-propos et présentation
Cette étude des phénomènes observés lorsque la lumière rencontre un obstacle, appelés diffraction, suit la démarche historique d'Augustin Fresnel. Elle utilise aussi les apports d'Émile Verdet, d'Henri Bouasse et Henri Bruhat qui ont su rendre attrayante et intelligible cette importante étude historique. Toute cette étude repose sur le principe d'Huygens-Fresnel. Elle donne lieu à toute une série d'approximations dont les physiciens ont le secret et qui déroutent les non-initiés, mais elles seront justifiées à posteriori par l'excellent accord entre les prévisions déduites des calculs et l'observation des phénomènes. Le principe d'Huygens-Fresnel n'apporte pas une réponse définitive et complète au problème de la diffraction, c'est une « hypothèse capable de fournir le plus grand nombre d'explications à partir du plus petit nombre de causes ».
Dans le mémoire sur la diffraction, Fresnel s'exprime ainsi (page 249 du tome I de ses œvres complètes) :|
« Si la nature s'est proposée de produire le maximum d'effets
avec le minimum de causes, c'est dans l'ensemble de ses lois
qu'elle a du résoudre ce grand problème.
Il est sans doute bien difficile de découvrir les bases de cette admirable économie, c'est-à-dire les causes les plus simples des phénomènes envisagés sous un point de vue aussi étendu. Mais, si ce principe général ne conduit pas immédiatement à la connaissance de la vérité il peut néanmoins diriger les efforts de l'esprit humain, en l'éloignant des systèmes qui rapportent les les phénomènes à un trop grand nombre de causes différentes, et en lui faisant adopter de préférence ceux qui appuyés sur le plus petit nombre d'hypothèses, sont les plus fécondes en conséquences. » |
Ces approximations conduisent à l'introduction et à l'étude des fonctions de Fresnel, dont nous pourrions aujourd'hui nous passer pour simuler avec un ordinateur ces phénomènes en appliquant le principe d'Huygens-Fresnel. Un exemple des franges observées lors de la diffraction par un bord d'écran rectiligne est donné par la figure 2. Fresnel avait calculé les tables des fonctions éponymes afin de vérifier ses hypothèses, pour rester dans l'état d'esprit des savants de cette époque les simulations numériques de cet article utilisent aussi les mêmes tables. Cette étude dédiée à Augustin Fresnel n'utilise que les outils mathématiques disponibles au XIXeS. Pour une vision moderne de l'optique ondulatoire faisant usage des complexes et de la transformée de Fourier notamment, on peut consulter le cours d'optique d'Éric Aristidi, professeur à l'université de Nice.
Le début du texte historique du mémoire de Fresnel sur la diffraction (dans les œuvres complètes, tome 2, cette introduction est rédigée de manière un peu différente 1) :
|
« Lorsque l'on fait entrer la lumière dans une chambre obscure par un très-petit trou, on remarque que les ombres des corps ainsi éclairés, au lieu d'être terminées nettement, sont bordées à l'extérieur de franges de diverses nuances et de différentes largeurs. Si le corps opaque est suffisamment étroit, quoique beaucoup moins que le point lumineux, et que l'on reçoive l'ombre à une distance assez considérable, on verra dans son intérieur des bandes obscures et brillantes qui la partagent en intervalles égaux, et qui sont colorées comme les premières. Avant d'exposer les lois suivant lesquelles les franges tant extérieures qu'intérieures varient de largeur, je vais rendre compte des observations qui me les ont fait découvrir. Pour obtenir le point éclairant, je me servais d'abord d'un très-petit trou pratiqué dans une feuille d'étain, et sur lequel je rassemblais beaucoup de lumière à l'aide d'une grande lentille ; mais le mouvement du soleil déplaçait promptement le foyer, et chaque observation ne pouvait durer qu'un instant. Enfin j'ai employé le moyen que M. Arago m'avait indiqué, et qui m'a parfaitement réussi. J'ai adapté à l'ouverture du volet de ma chambre obscure une lentille très-convexe, sur laquelle un miroir renvoyait les rayons solaires ; l'image formée au foyer était alors extrêmement resserrée, à cause de la grande convexité de la lentille, et produisait des franges colorées comme le point lumineux qu'on obtient à l'aide d'un très-petit trou. La lentille que j'ai employée a 12 millimètres de foyer ; elle donnait des franges assez nettes tant que le corps opaque n'en était pas éloigné de plus de 50 centimètres ; mais lorsque je les rapprochais davantage, ces franges devenaient très-vagues et ne pouvaient plus être mesurées assez exactement. N'ayant pas à ma disposition, pendant mes premiers essais, de lentille plus forte, j'eus recours à un globule de miel que je déposai sur un petit trou pratiqué dans une feuille de cuivre. éclairé par ce globule, le fil de fer dont je mesurais les franges en produisait encore de fort nettes, même lorsqu'il n'était plus qu'à un centimètre du point lumineux. Il est inutile d'ajouter que les lentilles de verre d' un très-court foyer, dont je me suis servi depuis, font le même effet. Pour reconnaître si les corps, dans le phénomène de la diffraction, agissent sur la lumière à des distances aussi considérables que le suppose Newton, j'ai cherché à observer les franges extérieures le plus près possible de leur origine ; mais comme, en recevant l'ombre sur un carton, il est difficile d'approcher assez l'œil pour les bien distinguer sans intercepter la lumière incidente, j'imaginai de la recevoir sur un verre dépoli, et de regarder par derrière avec une loupe. Or, je fus très étonné de voir au-delà des bords du verre des franges absolument semblables à celles qui étaient peintes sur sa surface. » |

|
| Figure 3 : diffraction par un trou carré. |

|
| Figure 4 : diffraction par un trou rectangulaire, de hauteur 5 fois plus grande que la largeur. |
Une remarquable interprétation du phénomène est faite dans le cours de Berkeley.
Pour interpréter le phénomène de la diffraction, Fresnel utilise le principe d'Huyghens : voici ce fameux principe tel que Fresnel l'énonce dans le tome II de ses œuvres complètes, page 59 :
| « Les vibrations d'une onde lumineuse dans chacun de ses points, peuvent être regardées comme la résultante des mouvements élémentaires qu'y enverraient au même instant, en agissant isolément, toutes les parties de cette onde considérée dans l'une quelconque de ses positions antérieures. » |
2. Diffraction par un bord d'écran rectiligne
Une source ponctuelle éclaire un bord d'écran rectiligne illimité d'un côté. On cherche à déterminer les franges de diffraction observées sur un écran placé au-delà de l'écran obstacle. Dans l'une des expériences de Fresnel a = 100, b = 799 (en mm) et λ = 0,638.10-6 m.
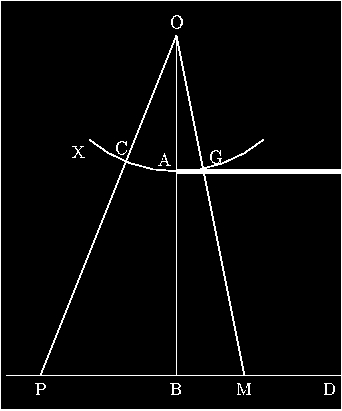
|
| Figure 6 : scéma page 322, tome V : leçons d'optique, de ses œuvres complètes. |
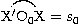 de rayon a, tangente en O0 au bord de l'écran (figure 7).
de rayon a, tangente en O0 au bord de l'écran (figure 7).
|
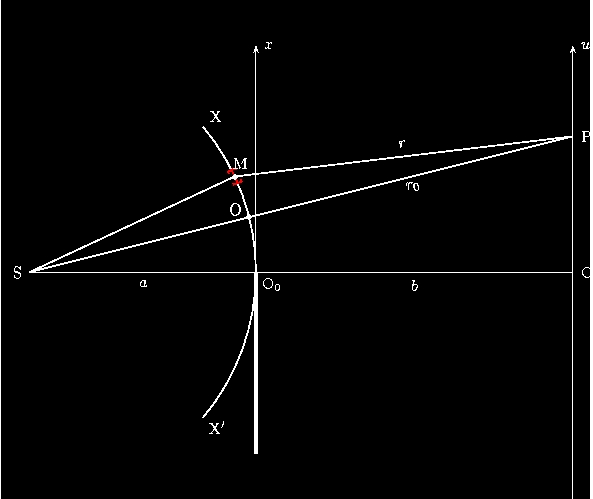
| Figure 7 : présentation géométrique de l'étude de la diffraction par un bord d'écran. |
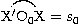 en O. On pose
en O. On pose
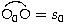 ,
, 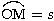 et
et 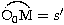 . Nous allons chercher
la contribution d'un arc élémentaire ds centré en M sur l'éclairement au point P.
La vibration lumineuse émise par la source est de la forme :
. Nous allons chercher
la contribution d'un arc élémentaire ds centré en M sur l'éclairement au point P.
La vibration lumineuse émise par la source est de la forme :
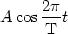
En M elle s'exprimera par :
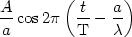
Et au point P, la contribution de l'arc élémentaire d svaudra :
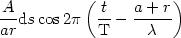
On considère comme négligeables les variations d'amplitude pour les différents
points du plan d'observation. Cette amplitude sera représentée par
K. On pose
r = r0 + 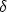 .
.
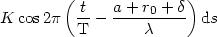
Le point P étant fixé et puisque nous cherchons la contribution des différents
points de l'onde circulaire  sur l'éclairement du point P,
a+ r0 reste constant, en
effectuant un changement de l'origine des temps l'état vibratoire s'écrit plus
simplement :
sur l'éclairement du point P,
a+ r0 reste constant, en
effectuant un changement de l'origine des temps l'état vibratoire s'écrit plus
simplement :
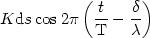
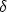 représente la différence de marche en P entre les ondes émises par O et M.
représente la différence de marche en P entre les ondes émises par O et M.
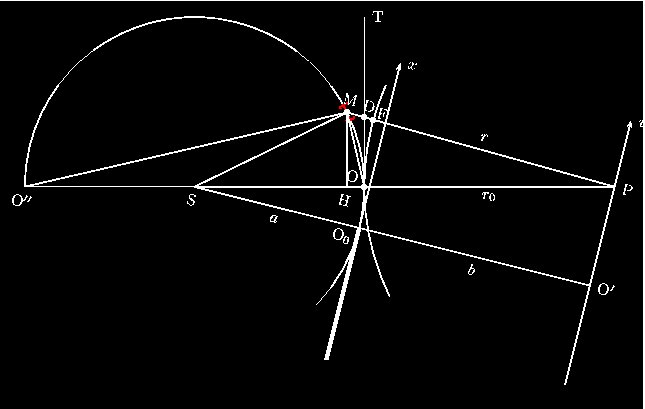
|
Figure 8 : calcul de la différence de marche 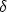 = d2 - d1 = MD + DF = d2 - d1 = MD + DF
|
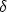 . Je suivrais la méthode développée par Henri
Bouasse dans son livre Diffraction, en suivant le schéma de la figure
8. La méthode exposée par
Émile Verdet est donnée en annexe . Pour une meilleure compréhension, je fais
subir une rotation à la figure précédente afin d'amener la droite (SP)
horizontale. On complète la figure par la tangente en O et diverses constructions nécessaires aux
explications, en particulier par un arc de cercle centré en P de rayon
r0.
. Je suivrais la méthode développée par Henri
Bouasse dans son livre Diffraction, en suivant le schéma de la figure
8. La méthode exposée par
Émile Verdet est donnée en annexe . Pour une meilleure compréhension, je fais
subir une rotation à la figure précédente afin d'amener la droite (SP)
horizontale. On complète la figure par la tangente en O et diverses constructions nécessaires aux
explications, en particulier par un arc de cercle centré en P de rayon
r0.
Pour une meilleure lisibilité, les angles sont exagérément grands sur la figure. Les approximations suivantes sont adoptées (voir Figure 8) :
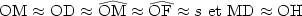
Dans le triangle rectangle O''MO, en utilisant une relation classique :
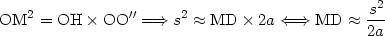
Opérons de la même manière pour calculer DF, on trouve :
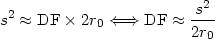
On en déduit le retard
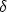 :
:
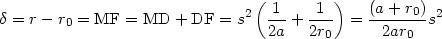
La contribution de l'arc élémentaire ds centré en M à l'état vibratoire du point P s'écrit :
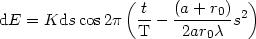
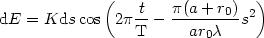
On définit la variable auxiliaire
 :
:
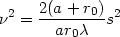
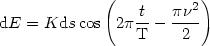
L'état de la vibration lumineuse au point P sera obtenue en faisant la somme de
tous les dE qui sont les contributions des différentes arcs élémentaires, suivant le
principe d' Huygens-Fresnel, de la partie découverte de l'écran qui va de
O0
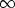 .
.
Posons  =
= 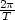 et d
et d =
=  ds avec :
ds avec :
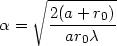
Appelons K' la nouvelle constante :
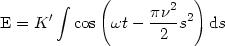
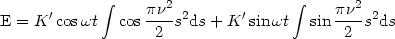
On pose :
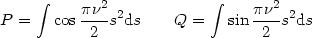
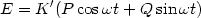
Nous n'écrivons plus le facteur constant K ', la vibration lumineuse est une grandeur proportionnelle à l'expression entre parenthèses. L'intensité lumineuse au point P est égale au carré de l'amplitude :
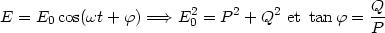
Elle est donnée par :
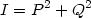
C( ) et S
(
) et S
( ) sont les intégrales de Fresnel :
) sont les intégrales de Fresnel :
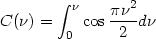
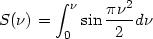
En examinant le tracé des deux courbes les représentant, nous constatons que
pour des valeurs de  grandes les deux intégrales prennent la même valeur
grandes les deux intégrales prennent la même valeur 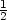 .
Pour calculer la valeur de ces intégrales lorsque
.
Pour calculer la valeur de ces intégrales lorsque
 est grand, on prendra
:
est grand, on prendra
:
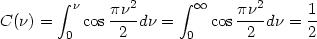
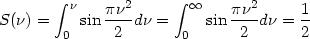
Il faut maintenant déterminer les bornes d'intégration : elles sont entre
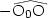 et
et
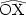 . X est le point de tangence mené par P.
. X est le point de tangence mené par P.
L'approximation suivante consiste à assimiler l'arc
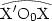 avec l'axe
x'Ox. Compte-tenu de la remarque précédente, il revient au même de prendre
comme bornes d'intégration -x et +
avec l'axe
x'Ox. Compte-tenu de la remarque précédente, il revient au même de prendre
comme bornes d'intégration -x et + 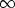 , soit pour la variable
, soit pour la variable
 entre -
entre -
 et
+
et
+ 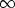 .
.
En remarquant que C(
 ) et S(
) et S( ) sont des fonctions impaires, on en déduit
:
) sont des fonctions impaires, on en déduit
:
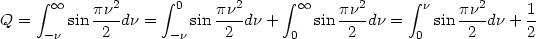
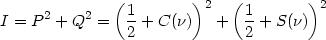
L'intensité, ou plutôt une grandeur qui lui est proportionnelle se calcule par :
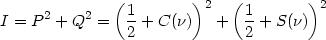
On se donne le point P par u et on en déduit
 .
.
La figure 9 représente les franges de diffraction en lumière blanche. Sur la figure 10 on a dessiné la courbe représentant les variations de l'intensité.

|
| Figure 9 : Figure de diffraction obtenue en lumière blanche, en grandeur réelle avec les paramètres a = 1 m et b = 10 m. Le trait noir représente la limite de l'ombre géométrique. |

|
| Figure 11 : Les franges sont d'autant plus larges que la longueur d'onde est grande. |