|
|
Résumé
Cet article est un modeste hommage à tous les scientifiques (géographes et mathématiciens) des siècles passés, à l’intelligence et l’ingéniosité dont ils font fait preuve afin de représenter la mappemonde terrestre en deux dimensions. Il existe des représentations multiples et très originales, et celle d’Édouard COLLIGNON, qui dans un mémoire publié en 1865 a compacté un hémisphère dans un carré, tout en conservant les aires est de plus très intéressante d’un point de vue didactique. Des renseignements sur cette projection se trouvent dans le livre Mémoire sur la représentation des surfaces et les projections géographiques de M.A.TISSOT, publié en 1881 à Paris par GAUTHIER-VILLARS et dans celui d’Henri BOUASSE : Géographie mathématique (1919), édité par DELAGRAVE. La partie qui va suivre est extraite des pages 168 et 169 de l’ouvrage de M.A.TISSOT. C’est un auteur dont les travaux sont une référence, même à notre époque, Eric W. WEISSTEIN le cite sur : http://mathworld.wolfram.com/ConformalProjection.html et son ellipse indicatrice 1 est toujours utilisée par les cartographes2 . Il est d’une très grande rigueur et présente une synthèse des différentes projections, mais il a un grand défaut : il contient très peu d’illustrations. Ce n’est pas le cas du livre d’Henri BOUASSE qui contient un grand nombre de schémas tous magnifiques 3. Malheureusement le premier livre est quasiment introuvable chez les bouquinistes d’internet, celui d’Henri BOUASSE apparaît de temps à autre dans leurs catalogues. Il y a dans l’un et l’autre des démonstrations merveilleuses et nous avons décidé d’illustrer celle de M.A.TISSOT concernant COLLIGNON à l’aide de schémas réalisés avec PSTricks, puisque c’est l’ouvrage le plus pauvre en figures. D’un point de vue historique, tous (explicitement ou non 4) font référence au Coup d’œil historique sur les projections des cartes géographiques de M. D’AVEZAC publié en 1863. |
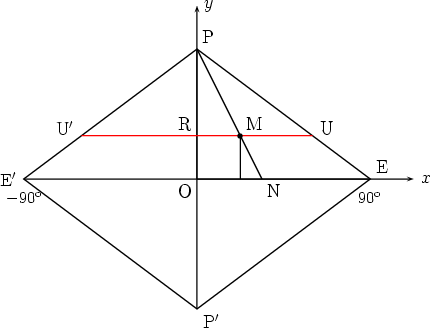
« Convenons de représenter le méridien qui limite un hémisphère
terrestre par le contour d’un losange PEP'E' (figure 1), la moitié
de l’équateur par une diagonale EE', et les deux pôles par les
extrémités P, P' de l’autre diagonale ; de plus, la moitié OP de cette
dernière étant désignée par n lorsqu’on prend le rayon du globe
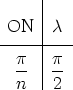
pour unité, supposons que la moitié OE de la première ait pour
longueur  , afin que la surface du losange soit égal à 2 , afin que la surface du losange soit égal à 2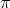 , comme
celle de l’hémisphère. À ces données correspondra une projection
hémicylindrique authalique qu’il s’agit d’obtenir. , comme
celle de l’hémisphère. À ces données correspondra une projection
hémicylindrique authalique qu’il s’agit d’obtenir.
« Soit UU' la projection de la latitude |
M.A.TISSOT développe ensuite, à partir de ses conclusions, les constructions géométriques – ce qui à son époque était la chose la plus importante, permettant de réaliser la projection souhaitée. Par contre ce qui nous intéresse, c’est d’obtenir les coordonnées sur le plan Oxy de la projection d’un point de la mappemonde. On se reportera à la figure 2, pour suivre les petits calculs qui permettent d’obtenir les coordonnées.
La corde de l’arc générateur de la calotte sphérique U'P vaut :
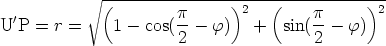
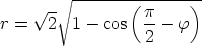
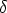 =
= 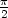 -
- 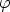 (colatitude).
(colatitude).
En utilisant la relation trigonométrique : 1 - cos 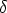 = 2 sin 2
= 2 sin 2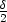 , la longueur de la
corde r vaut :
, la longueur de la
corde r vaut :
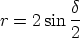
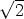 , écrivons donc le rapport :
, écrivons donc le rapport :
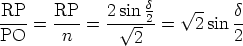
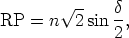
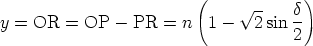
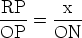

 pour la raison suivante : rappelons que OE =
pour la raison suivante : rappelons que OE =  , donc qu’on peut
établir la correspondance :
, donc qu’on peut
établir la correspondance :
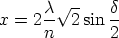
| Les projections méricylindriques authaliques à méridiens et parallèles rectilignes ont été imaginés en 1865 par M. Édouard COLLIGNON, qui considérant plus spécialement le cas où le contour de la carte serait formé d’un carré, a traité la question analytiquement et a déduit de ses formules les constructions géométriques données plus haut. |
On obtiendra un carré en posant que OE = OP, soit pour :
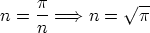
Bravo M.COLLIGNON !
Les deux figures ont été obtenues avec le script suivant :
\psset{maillage=true,n=1.77245,Fill=true,rivers=true,borders=trueUSA=true}
\begin{figure} \centering \hbox{\hspace{-2cm} \psset{xunit=0.75,yunit=0.75} \begin{pspicture}(-11,-11)(11,11) \Collignon \end{pspicture}} \caption{\label{HemisphereA}Hémisphère A} \end{figure} \begin{figure} \centering \hbox{\hspace{-2cm} \psset{xunit=0.75,yunit=0.75} \begin{pspicture}(-11,-11)(11,11) \Collignon[HemisphereA=false] \end{pspicture}} \caption{\label{HemisphereB}Hémisphère B} \end{figure} |
http://melusine.eu.org/syracuse/mluque/mappemonde/ Il faut indiquer le chemin des données dans la variable path. Cette variable contient le chemin des données sur mon disque dur :
path=C:/mappemonde/wdb
Il faut donc avant le \begin{document}, indiquer celui qui
correspond à votre configuration :
\psset{path=C:/mappemonde/wdb}
ou bien le modifier directement dans le fichier pst-collignon.tex.