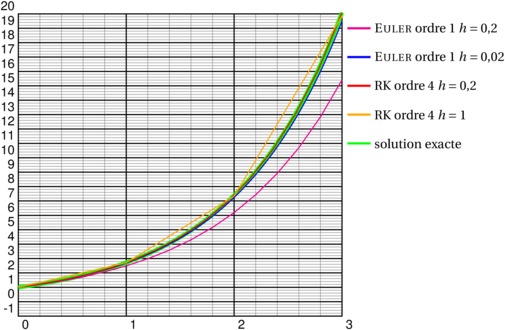
\psset{xunit=3, yunit=.4} \begin{pspicture}(0,-1)(3,20)\psgrid \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{3}{2.71828182846 x exp} \psplotequadiff[linecolor=magenta, plotpoints=16]{0}{3}{1}{} \psplotequadiff[linecolor=blue, plotpoints=151]{0}{3}{1}{} \psplotequadiff[linecolor=red, method=rk4, plotpoints=15]{0}{3}{1}{} \psplotequadiff[linecolor=Orange, method=rk4, plotpoints=4]{0}{3}{1}{} \psset{linewidth=2\pslinewidth} \rput*(3.3,19){\psline[linecolor=magenta](-.75cm,0)} \rput*[l](3.3,19){\small\textsc{Euler} ordre 1 $h=0{,}2$} \rput*(3.3,17){\psline[linecolor=blue](-.75cm,0)} \rput*[l](3.3,17){\small\textsc{Euler} ordre 1 $h=0{,}02$} \rput*(3.3,15){\psline[linecolor=red](-.75cm,0)} \rput*[l](3.3,15){\small RK ordre 4 $h=0{,}2$} \rput*(3.3,13){\psline[linecolor=Orange](-.75cm,0)} \rput*[l](3.3,13){\small RK ordre 4 $h=1$} \rput*(3.3,11){\psline[linecolor=green](-.75cm,0)} \rput*[l](3.3,11){\small solution exacte} \end{pspicture}
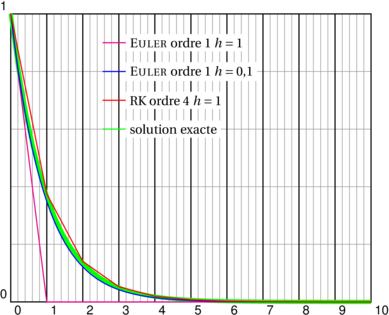
\def\Funct{neg} \psset{xunit=1, yunit=8} \begin{pspicture}(0,0)(10,1)\psgrid \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{10}{2.71828182846 x neg exp} \psplotequadiff[linecolor=magenta, plotpoints=11]{0}{10}{1}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=101]{0}{10}{1}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=11]{0}{10}{1}{\Funct} \rput*(3.3,.9){\psline[linecolor=magenta](-.75cm,0)} \rput*[l](3.3,.9){\small\textsc{Euler} ordre 1 $h=1$} \rput*(3.3,.8){\psline[linecolor=blue](-.75cm,0)} \rput*[l](3.3,.8){\small\textsc{Euler} ordre 1 $h=0{,}1$} \rput*(3.3,.7){\psline[linecolor=red](-.75cm,0)} \rput*[l](3.3,.7){\small RK ordre 4 $h=1$} \rput*(3.3,.6){\psline[linecolor=green](-.75cm,0)} \rput*[l](3.3,.6){\small solution exacte} \end{pspicture}
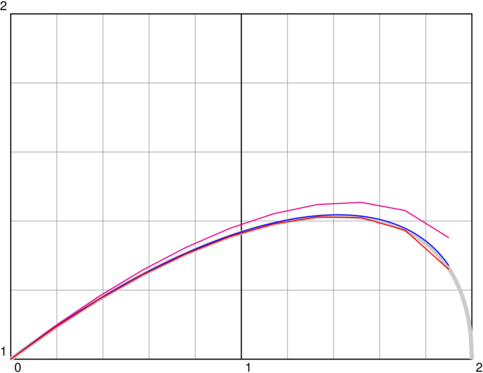
%\psset{xunit=3.2, showpoints=false} \psset{xunit=6.4, yunit=9.6, showpoints=false} %\begin{pspicture}(-2,-1)(2,2)\psgrid \begin{pspicture}(0,1)(2,2)\psgrid %\psplot[linewidth=4\pslinewidth,linecolor=lightgray]{-2}{-1.8}{x dup dup mul 4 exch sub sqrt add 2 div} %\psplot[linewidth=4\pslinewidth,linecolor=lightgray]{-1.8}{1.8}{x dup dup mul 4 exch sub sqrt add 2 div} \psplot[linewidth=4\pslinewidth,linecolor=lightgray]{0}{1.8}{x dup dup mul 4 exch sub sqrt add 2 div} \psplot[linewidth=4\pslinewidth,linecolor=lightgray]{1.8}{2}{x dup dup mul 4 exch sub sqrt add 2 div} \newcommand{\InitCond}{1} \newcommand{\Func}{x mul 2 exch sub 4 x dup mul sub div} \psplotequadiff[linecolor=magenta, plotpoints=11]{0}{1.9}{\InitCond}{\Func} \psplotequadiff[linecolor=blue, plotpoints=101]{0}{1.9}{\InitCond}{\Func} \psplotequadiff[linecolor=red, method=rk4, plotpoints=11]{0}{1.9}{\InitCond}{\Func} \end{pspicture}
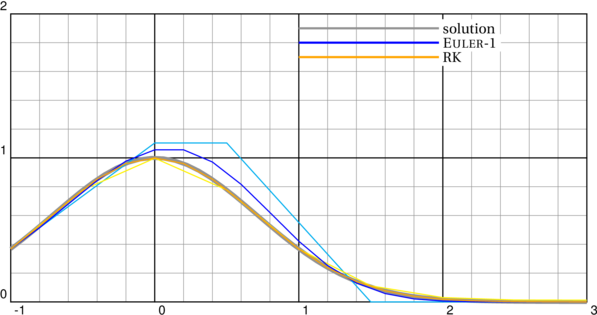
\psset{unit=4} \begin{pspicture}(-1,0)(3,2)\psgrid \psplot[linewidth=4\pslinewidth,linecolor=gray]{-1}{3}{2.71828182846 x dup mul neg exp} \psset{plotpoints=9} \psplotequadiff[linecolor=cyan]{-1}{3}{1 2.71828182846 div}{x -2 mul mul} \psplotequadiff[linecolor=yellow, method=RK4]{-1}{3}{1 2.71828182846 div}{x -2 mul mul} \psset{plotpoints=21} \psplotequadiff[linecolor=blue]{-1}{3}{1 2.71828182846 div}{x -2 mul mul} \psplotequadiff[linecolor=Orange, method=RK4]{-1}{3}{1 2.71828182846 div}{x -2 mul mul} \psset{linewidth=2\pslinewidth} \rput*(2,1.7){\psline[linecolor=Orange](-1,0)} \rput*[l](2,1.7){RK} \rput*(2,1.8){\psline[linecolor=blue](-1,0)} \rput*[l](2,1.8){\textsc{Euler}-1} \rput*(2,1.9){\psline[linecolor=gray](-1,0)} \rput*[l](2,1.9){solution} \end{pspicture}
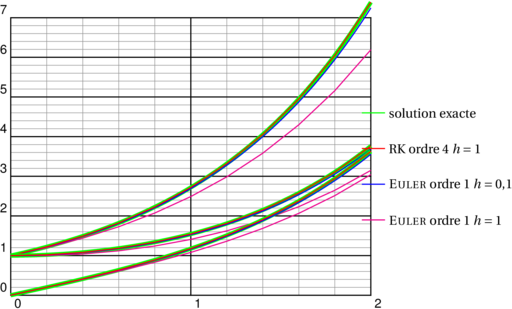
\def\Funct{exch} \psset{xunit=5, yunit=1.1} \begin{pspicture}(0,0)(2,7)\psgrid %%e^x \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{2}{2.71828182846 x exp} \psplotequadiff[linecolor=magenta, plotpoints=11]{0}{2}{1 1}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=101]{0}{2}{1 1}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=11]{0}{2}{1 1}{\Funct} %%ch(x) \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{2}{2.71828182846 dup x exp exch x neg exp add 2 div} \psplotequadiff[linecolor=magenta, plotpoints=11]{0}{2}{1 0}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=101]{0}{2}{1 0}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=11]{0}{2}{1 0}{\Funct} %%sh(x) \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{2}{2.71828182846 dup x exp exch x neg exp sub 2 div} \psplotequadiff[linecolor=magenta, plotpoints=11]{0}{2}{0 1}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=101]{0}{2}{0 1}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=11]{0}{2}{0 1}{\Funct} \rput*(2.1,1.9){\psline[linecolor=magenta](-.75cm,0)} \rput*[l](2.1,1.9){\small\textsc{Euler} ordre 1 $h=1$} \rput*(2.1,2.8){\psline[linecolor=blue](-.75cm,0)} \rput*[l](2.1,2.8){\small\textsc{Euler} ordre 1 $h=0{,}1$} \rput*(2.1,3.7){\psline[linecolor=red](-.75cm,0)} \rput*[l](2.1,3.7){\small RK ordre 4 $h=1$} \rput*(2.1,4.6){\psline[linecolor=green](-.75cm,0)} \rput*[l](2.1,4.6){\small solution exacte} \end{pspicture}
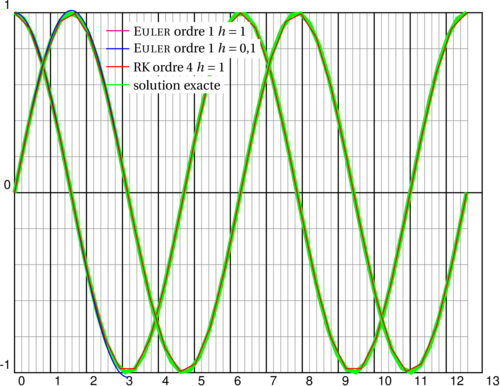
\def\Funct{exch neg} \psset{xunit=1, yunit=5}%%4pi=12.5663706144 \def\quatrepi{12.5663706144} \begin{pspicture}(0,-1)(\quatrepi,1)\psgrid %%cos(x) \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{\quatrepi}{x 3.1415926 div 180 mul cos} %\psplotequadiff[linecolor=magenta, plotpoints=31]{0}{\quatrepi}{1 0}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=201]{0}{3.1415926}{1 0}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=31]{0}{\quatrepi}{1 0}{\Funct} %%sin(x) \psplot[linewidth=4\pslinewidth, linecolor=green]{0}{\quatrepi}{x 3.1415926 div 180 mul sin} %\psplotequadiff[linecolor=magenta, plotpoints=31]{0}{\quatrepi}{0 1}{\Funct} \psplotequadiff[linecolor=blue, plotpoints=201]{0}{3.1415926}{0 1}{\Funct} \psplotequadiff[linecolor=red, method=rk4, plotpoints=31]{0}{\quatrepi}{0 1}{\Funct} \rput*(3.3,.9){\psline[linecolor=magenta](-.75cm,0)} \rput*[l](3.3,.9){\small\textsc{Euler} ordre 1 $h=1$} \rput*(3.3,.8){\psline[linecolor=blue](-.75cm,0)} \rput*[l](3.3,.8){\small\textsc{Euler} ordre 1 $h=0{,}1$} \rput*(3.3,.7){\psline[linecolor=red](-.75cm,0)} \rput*[l](3.3,.7){\small RK ordre 4 $h=1$} \rput*(3.3,.6){\psline[linecolor=green](-.75cm,0)} \rput*[l](3.3,.6){\small solution exacte} \end{pspicture}
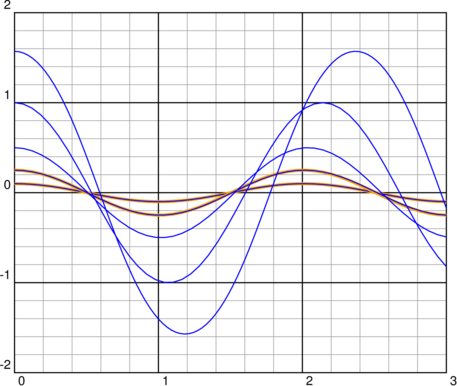
\def\Func{exch 3.1415926 div 180 mul sin -9.8 mul} \psset{yunit=2.5, xunit=4} \begin{pspicture}(0,-2)(3,2)\psgrid \psplot[linewidth=3\pslinewidth, linecolor=Orange]{0}{3}{x 3.1415926 div 180 mul 9.8 sqrt mul cos .1 mul} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=50]{0}{3}{.1 0}{\Func} \psplot[linewidth=3\pslinewidth, linecolor=Orange]{0}{3}{x 3.1415926 div 180 mul 9.8 sqrt mul cos .25 mul} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=50]{0}{3}{.25 0}{\Func} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=50]{0}{3}{.5 0}{\Func} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=50]{0}{3}{1 0}{\Func} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=100]{0}{3}{3.1415926 2 div 0}{\Func} \end{pspicture}
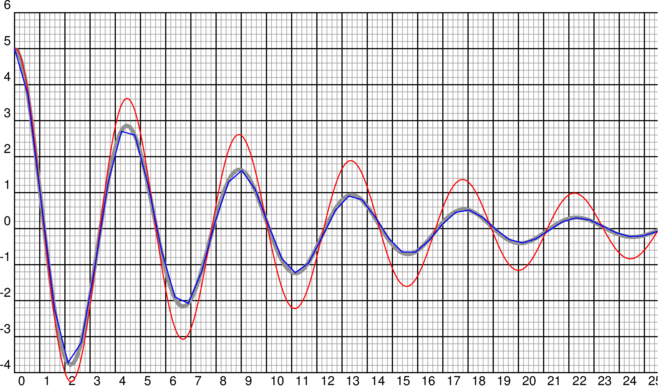
\psset{xunit=.7} \begin{pspicture}(0,-4)(26,6)\psgrid \psplot[plotpoints=200, linewidth=4\pslinewidth, linecolor=gray]{0}{26}{2.71828182846 x -8 div exp x 127 sqrt 8 div mul 180 mul 3.1415926535 div dup cos 5 mul exch sin 127 sqrt div 5 mul add mul} \psplotequadiff[linecolor=red, plotpoints=500]{0}{26}{5 0} {dup 3 1 roll -4 div exch 2 mul sub} \psplotequadiff[linecolor=blue, method=rk4, plotpoints=50]{0}{26}{5 0} {dup 3 1 roll -4 div exch 2 mul sub} \end{pspicture}