cour_019.tex

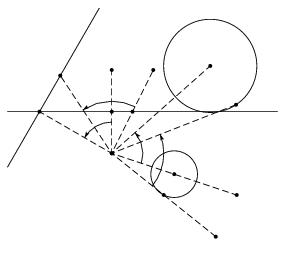
\paragraphe {Similitudes $(z \mapsto az, a\in \cset )$ }
 
On appelle {\sl similitude\/} de centre $O$, de rapport $k$ et d'angle
$\theta $ la composée de l'homothétie de centre $O$ et de rapport $k$
avec la rotation de centre $O$ et d'angle $\theta $. On note $S_{O,
\theta , k} = h_{O, k} \circ R_{O, \theta } = R_{O, \theta } \circ
h_{O, k}$ (l'ordre de la composition n'a pas d'importance).
 
On considère $f$ l'application de $\cset $ dans $\cset $ définie par $z
\mapsto az$ où $k$ est un nombre {\bf complexe} quelconque. Pour
chaque complexe $z$ donné, on note $M$ le point image de $z$, et $M'$
l'image de $z' = f (z)$ dans le plan complexe. 
 
Alors l'application $M \mapsto M'$ ainsi définie est la similitude de
centre $O$ (l'origine du repère), de rapport $\theta = \arg (a)$ et de
rapport $k= |a|$.
 
\tmpdimen 265 pt
\epsfysize .8 \tmpdimen
 
\bgroup
\catcode`\|=12
\input \path pstricks/pstricks.tex           %% PSTricks
$$\displaylines {
   %% xsize: 100.45 mm, 285.83 pt
   %% ysize: 93.13 mm, 265 pt
   \psset{unit=.8pt}
   \pspicture(-195,-132.5)(90.83,132.5)
   \psset{xunit=20.83,yunit=20.83}
   \rput(-2.5,1){\superboxepsillustrate {cour_019.ps}}
   \rput[u](-4,0){$O$}
   \rput[ur](-4,2){$M_1$}
   \rput[ul](-3,2){$M_2$}
   \rput[ur](-4,4){$M'_1$}
   \rput[ul](-2,4){$M'_2$}
   \rput[r](-7.5,2.7){$M''_1$}
   \rput[br](-6.5,4){$M''_2$}
   \rput[r](-1.5,-2){$N$}
   \rput[r](-1,-1){$\Omega $}
   \rput[r](1,-4){$N'$}
   \rput[l](2.2,2.4){$N''$}
   \rput[r](2,-2){$\Omega '$}
   \rput[l](1,4.5){$\Omega ''$}
   \endpspicture
\cr
   \tresultat {Images d'une droite et d'un cercle par la similitude
   $z\mapsto 2 e^{i\pi /3} z$}
\cr
}$$
\egroup
 
Une telle similitude conserve le parallélisme et les angles, mais multiplie
les distances par $|k|$.