cour_020.tex

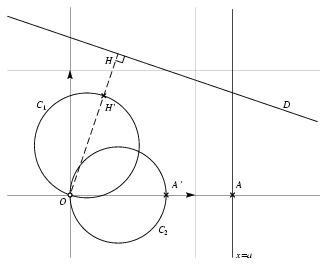
\paragraphe {Inversion $\displaystyle (z \mapsto {1\over \overline z})$ }
 
On appelle {\sl inversion\/} de centre $O$ et de puissance $1$
l'application qui à tout point $M$, autre que $O$, associe le point
$M'$ tel que~:
 
\item {$\bullet $} $OM \times OM' = 1$
 
\item {$\bullet $} $M'$ appartient à la demi-droite issue de $O$
passant par $M$.
 
On considère $f$ l'application de $\cset $ dans $\cset $ définie par
$\displaystyle z \mapsto {1\over \overline z}$, et on note  $M$ l'image de $z$
et $M'$ l'image de $z' = f (z)$ dans le plan complexe. 
Alors l'application $M \mapsto M'$ ainsi définie est l'inversion de
centre $O$ et de puissance $1$.
 
Pour construire l'image d'un point $M$ d'affixe, on utilise le fait que si 
$$
   z = [r, \theta ] = re^{i\theta }
      \qquad {\rm alors} \qquad
   {1\over \overline z} = \left[ {1\over r}, \theta \right] = {1\over r}e^{i\theta }.
$$
 
Reste à savoir (et on l'admettra) que~:
 
\item {$\bullet $} L'image par l'inversion de centre $O$ et de
puissance~1 d'une droite ne passant pas par $O$ est un cercle
privé d'un point.
 
\item {$\bullet $} L'image par l'inversion de centre $O$ et de
puissance~1 de la droite d'équation $x = a$ ($a\neq 0$) est le cercle
de centre $\Omega (1/2a, 0)$, de rayon $1/2a$, privé du point $O$.
 
Ainsi, dans l'exemple ci-dessous on a tracé les cercles $C_1$ et
$C_2$, images respectives des droites $D$ et $x=a$ par l'inversion de
centre $O$ et de puissance~$1$.
\epsfxsize = 80mm
$$\displaylines {
   \superboxepsillustrate {cour_020.ps}
\cr
   \tresultat {Images de 2~droite par l'inversion de centre $O$ de
   puissance 1}
\cr
}$$
 
%% ==================
 
\paragraphe {Inversion complexe $\displaystyle (z \mapsto {1\over z})$ }
 
On considère $f$ l'application de $\cset $ dans $\cset $ définie par
$\displaystyle z \mapsto {1\over z}$, et on note  $M$ l'image de $z$
et $M'$ l'image de $z' = f (z)$ dans le plan complexe. 
Alors l'application $M \mapsto M'$ ainsi définie est l'inversion de
centre $O$ et de puissance $-1$, parfois aussi appelé {\sl inversion complexe}.
 
Pour construire l'image d'un point $M$ d'affixe, on utilise le fait que si 
$$
   z = [r, \theta ] = re^{i\theta }
      \qquad {\rm alors} \qquad
   {1\over z} = \left[ {1\over r}, - \theta \right] = {1\over r}e^{-i\theta }.
$$
 
Géométriquement, la transformation ainsi définie est la composée de
l'inversion de centre $O$ et de puissance~1 avec la symétrie orthogonale
d'axe $Ox$.