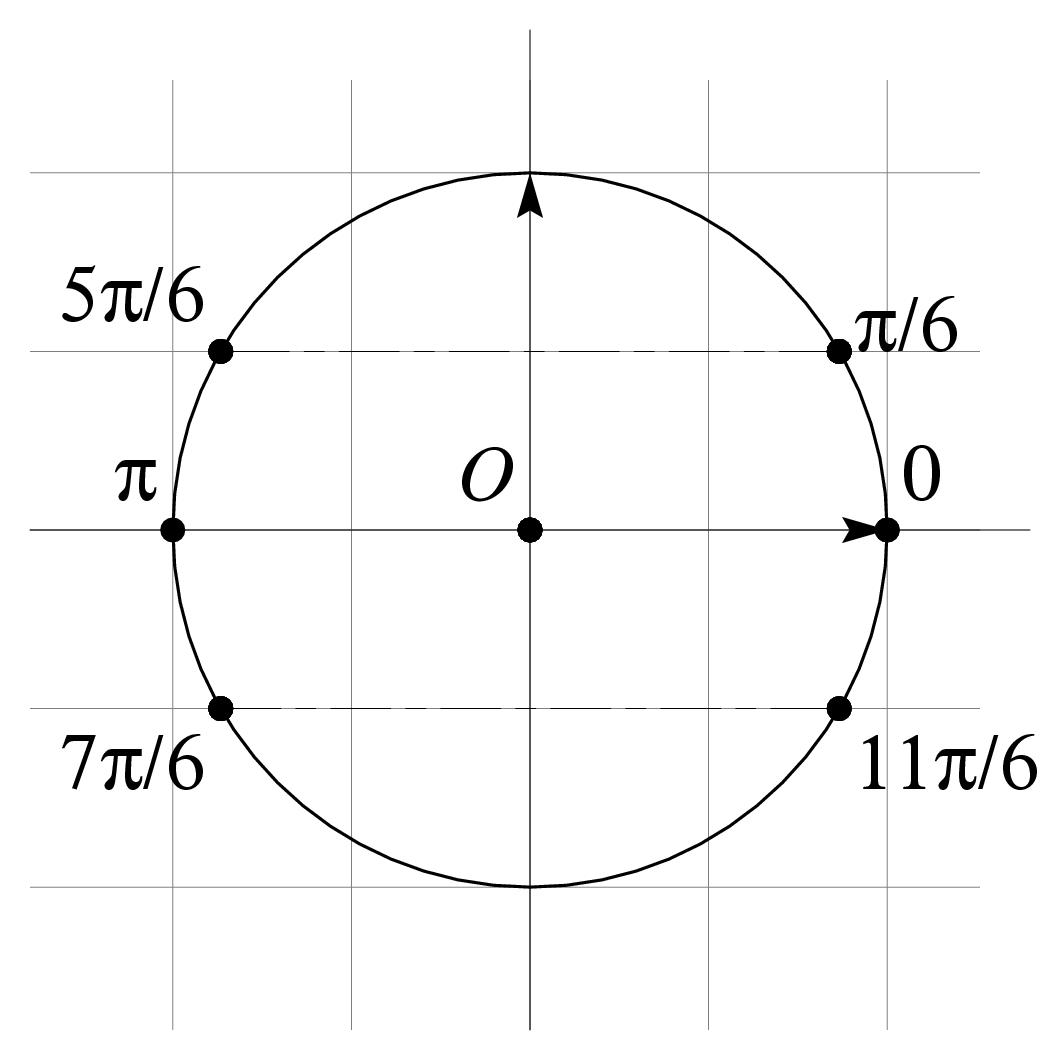
\exo {\' Equation trigonométrique et linéarisation} Le but de cet exercice est la résolution dans l'intervalle $[0, 2\pi [$ de l''équation $$ 2 \sin x - \sin 3x = 0. $$ \itemnum Soit $x$ un nombre réel~: \itemitemalph Développer $(e^{ix} - e^{-ix})^3$ et montrer que $$ (e^{ix} - e^{-ix})^3 = (e^{3ix} - e^{-3ix}) - 3(e^{ix} - e^{-ix}). $$ \itemitemalph Transformer l'égalité précédente à l'aide des formules d'Euler, et en déduire que~: $$ 4 \sin ^3 x - \sin x = 2 \sin x - \sin 3x. $$ \itemnum Résoudre dans l'intervalle $[0, 2\pi [$ les équations suivantes~: $$ \alph \ \sin x = 0, \phantom {{1\over 2}} \qquad \qquad \alph \ \sin x = {1\over 2}, \qquad \qquad \alph \ \sin x = -{1\over 2}. $$ \itemnum En déduire les solutions appartenant à l'intervalle $[0, 2\pi [$ de l'équation $$ 2 \sin x - \sin 3x = 0. $$ \finexo \corrige {} \itemalphnum On utilise la formule $(a+b)^3 = a^3 + 3a^2b + 3 ab^2 + b^3$ . En prenant $a = e^{ix}$ et $b = - e^{-ix}$, il vient $$\eqalign{ (e^{ix} - e^{-ix})^3 &= e^{3ix} - 3 e^{2ix}e^{-ix} + 3 e^{ix}e^{-2ix} - e^{-3ix} \cr &= e^{3ix} - 3 e^{2ix-ix} + 3 e^{ix-2ix} - e^{-3ix} \cr &= e^{3ix} - 3 e^{ix} + 3 e^{-ix} - e^{-3ix} \cr &= (e^{3ix} - e^{-3ix}) - 3( e^{ix} - e^{-ix}) \cr }$$ \itemalph En utilisant la relation d'Euler~: $2i \sin \theta = e^{i\theta} - e^{-i \theta}$, cette dernière égalité s'écrit $$\displaylines{ (2i \sin x)^3 = 2i \sin (3x) - 3 \times 2i \sin x \qquad {\rm soit} \qquad -8i \sin^3 x = 2i \sin (3x) - 6i \sin x \cr \qquad {\rm soit\ encore} \qquad \dresultat{4 \sin^3 x = -\sin (3x) + 3 \sin x}, \hbox {d'où l'égalité demandée.} \cr }$$ \itemnum En regardant sur le cercle trigonométrique, on trouve facilement les solutions sur $[0, 2\pi[$ de ces trois équations~: \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/algebre/complex/} \epsfxsize 30mm $$ \vcenter {% \hbox {\alph \ \tresultat {2 solutions~: $0$ et $\pi $}} \bigskip \hbox {\alph \ \tresultat {2 solutions~: $\pi /6$ et $5\pi /6$}} \bigskip \hbox {\alph \ \tresultat {2 solutions~: $7\pi /6$ et $11\pi /6$}} } \qquad \qquad \vcenter {\superboxepsillustrate {euler_003.ps}} $$ \itemnum Finalement, on a $$\displaylines{ (E)~: \quad2 \sin x - \sin (3x) = 0 \quad \Longleftrightarrow \quad 4 \sin^3 x - \sin x = 0 \cr \quad \Longleftrightarrow \quad \sin x \left( 4\sin^2 x - 1 \right) = 0 \quad \Longleftrightarrow \quad \sin x (2 \sin x - 1) (2 \sin x + 1) = 0 \cr }$$ Donc $x$ est solution de l'équation $(E)$ si et seulement si $$ \sin x = 0 \qquad {\rm ou} \qquad \sin x = {1\over2} \qquad {\rm ou} \qquad \sin x = -{1\over2}. $$ En vertu des questions précédentes, les solutions dans $[0, 2\pi[$ sont donc \dresultat{0, {\pi \over6}, {5\pi \over6}, {7\pi \over6}, {11\pi \over6}, \pi }. \fincorrige