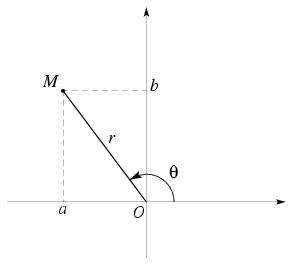
\sparagraphe {Forme trigonométrique, forme exponentielle} \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/algebre/complex/} \epsfxsize = 60mm \rightsuperboxepsillustrate {cour_006.ps}{-15} % Soit le nombre complexe $z = a+ib$ et son point image $M$ dans le plan rapporté à un repère orthonormal $(O, \vec u, \vec v)$. Le point $M$, s'il est différent de l'origine $O$, est entièrement déterminé par les données de la distance $r$ et de l'angle $\theta $, où $$ r = OM \qquad {\rm et} \qquad \theta = \widehat {(\vec u, \overrightarrow {OM})}. $$ Ce qui nous donne une autre écriture pour le nombre complexe $z$. On notera $$ \dresultat {z = [r, \theta ]} \qquad {\rm ou} \qquad \dresultat {z = r e^{i\theta }} $$ qui sont respectivement appelées {\sl forme trigonométrique\/} et {\sl forme exponentielle\/} du nombre complexe $z$. On appelle {\sl module\/} de $z$, et on note $|z|$, le nombre $|z| = r$. On appelle {\sl argument\/} de $z$, et on note $\arg (z)$, toute mesure de l'angle $\theta $. L'argument d'un nombre complexe n'est donc défini qu'à $2k\pi $ près. On en donne généralement la {\sl détermination principale\/} qui est la mesure appartenant à l'in\-ter\-val\-le $]-\pi , \pi ]$. En conséquence, les nombres $z = [r, \theta ]$ et $z' = [r', \theta ']$ sont égaux si et seulement si $$ \dresultat {r = r'} \qquad {\rm et} \qquad \dresultat {\theta = \theta' + 2k\pi }, \quad {\rm où} \quad k \in \zset . $$ Pour passer d'une écriture à une autre, on utilise les résultats suivants~: si $z = a + ib$ , on a $$\resultat { |z| = r = \sqrt {a^2 + b^2}. }$$ et en considérant les projections orthogonales du point $M$ sur les axes de coordonnées, on obtient les relations $$ a = r \cos \theta, \qquad {\rm et} \qquad b = r \sin \theta . $$ On peut alors déterminer $\theta $ en utilisant le fait que $$ \dresultat {\cos \theta = {a \over r}} \qquad {\rm et} \qquad \dresultat {\sin \theta = {b \over r}} $$ Réciproquement, si on a la forme exponentielle $z = r e^{i\theta }$, on détermine la forme algébrique avec la relation~: $$ \dresultat {z = re^{i\theta } = r (\cos \theta + i \sin \theta ) = a + ib }. $$ {\bf Remarque~:} On a donc en particulier \dresultat {e^{i\theta } = \cos \theta + i \sin \theta }.