Fichier 1202.jps — Modifié le 22 Mars 2007 à 17 h 59
Source
%% PhS
%% fig_S_cours_ch03_equations_differentieles_02_v01.jps
40 setxunit
-7 7 setxrange
-7 7 setyrange
tracerepere
marks
/Gx_min -3 def
/Gx_max 3 def
/Gy_min -3 def
/Gy_max 3 def
/pas_x 0.5 def
/pas_y 0.5 def
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% definitions des couleurs
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
/coul1 {120 255 div 70 255 div 9 255 div setrgbcolor} def
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% procédures
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% définition du champ de vecteur
/vect_t_y {
2 dict begin
/y exch def
/t exch def
t 1 add 2 div y mul
1 exch
end
} def
%% parametrage de la courbe
/xdet {
1 dict begin
/t exch def
t
end
} def
/ydet {
1 dict begin
/t exch def
t 2 div dup dup mul add Exp 0.5 mul
end
} def
%% tracé du champ de vecteurs
coul1
Gx_min pas_x Gx_max { 2 dict begin
/c_x exch def
Gy_min pas_y Gy_max {
/c_y exch def
1 setlinewidth
orange [c_x c_y] {times} plot
coul1
0.5 setlinewidth
c_x c_y
c_x c_y c_x c_y vect_t_y
c_x c_y vect_t_y norme 0.4 exch div mulv addv
(->) line
} for
end
} for
%% tracé de la courbe intégrale
1 setlinewidth
rouge
continu
-4 2.2 settrange
{xdet} {ydet} courbeparam
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% texte
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
setTimesItalic
noir
<latex>
O
</latex>
0 0 [1.5 dup] dltexlabel
<latex>
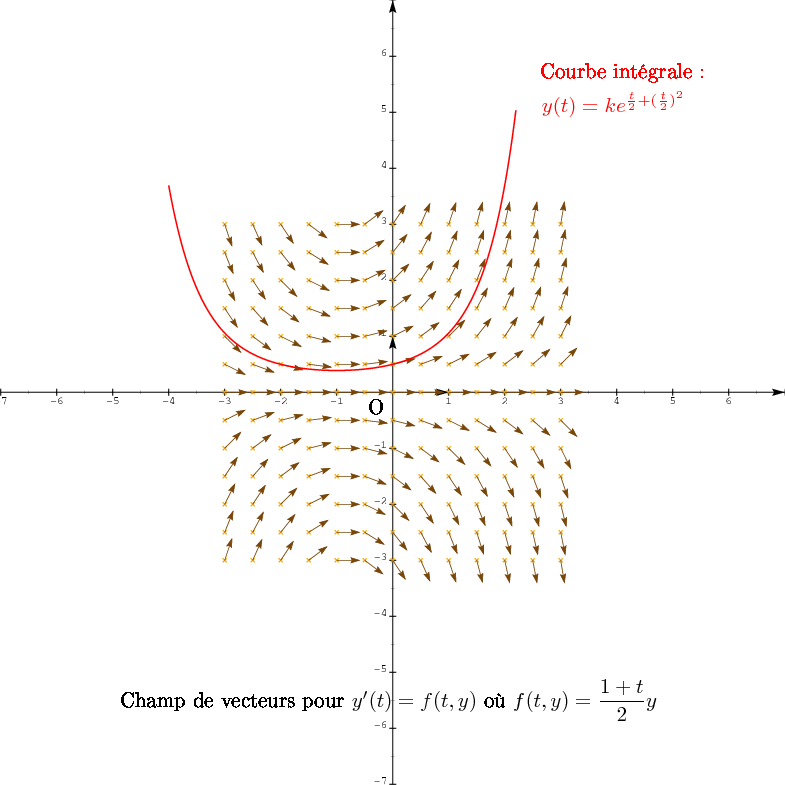
Champ de vecteurs pour
$ y'(t)=f(t,y) $ où
$ f(t,y)=\displaystyle\frac{1+t}{2}y $
</latex>
-5 -5 [1.5 dup] drtexlabel
rouge
<latex>
Courbe intégrale~:
</latex>
2.5 6 [1.5 dup] drtexlabel
<latex>
$ y(t)=ke^{\frac{t}{2}+(\frac{t}{2})^2} $
</latex>
2.5 5.5 [1.5 dup] drtexlabel