%% auteur : 
%% jpv, d'apres un exemple original de D. Rodriguez (en pstricks)
%% http://melusine.eu.org/syracuse/pstricks/rodriguez/eqdf/
%% et en partant du code de JJ Bataille

5 setxyrapport
100 setxunit
-.5 6 setxrange
-3 20 setyrange

0 3 setxrange
0 20 setyrange

/quadrillagewidth [.5] def
[.2 .2] {.8 setgray} Quadrillage
[1 1] {.2 setgray} Quadrillage

ticks
marks
traceaxes

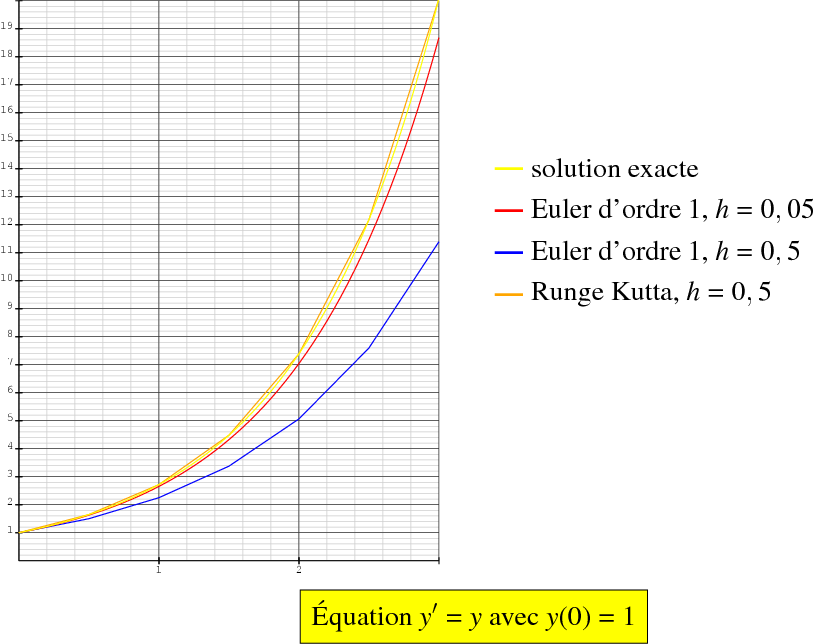
%%%% L'équation différentielle y'=y avec la condition initiale y(0)=1 sur lintervalle [0;3]%%%%

%%% La foction solution%%%%%%%%%
/f {setxvar
#rpn#   Exp (x)
} def

%%%%%%%%% Paramètres pour l'approx par la méthode d'Euler%%%%%%%
/pas {2 nb div} def  %%%calcul du pas de la subdivision
/x0 {0} def          %% coordonnees du point a l'origine
/y0 {1} def
/a  {0} def          %% intervalle de calcul = [a;b]
/b  {3} def

%%%%% L'exécutable qui calcule (x_k+1, y_k+1) en fonction de (x_k,y_k)%%%%%%

/F {
2 dict begin
   /y exch def
   /x exch def
#rpn# y
end
} def

%% %%%%%%%% première execution et tracé en rouge %%%%%%%%%%
/pas .5 def
bleu
[a b {F} x0 y0 pas Euler ] ligne  

/pas .05 def
rouge
[a b {F} x0 y0 pas Euler ] ligne  

/pas .5 def
orange
[a b {F} x0 y0 pas Rungekutta ] ligne  

jaune
a b {f} Courbe

%%%%%%%%% Labels %%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%% Label 1 %%%

<tex>
\' Equation $y' = y$ avec $y (0) = 1$
</tex>

%% placement du label 1
noir
/fillstyle {jaune fill} def
boxit
3.25 -2 [2 dup] cctexlabel

%% legende
2 setlinewidth
/pas -1.5 def
/longueur .2 def
/xd 3.4 def
/h1 14 def
/h2 h1 pas add def
/h3 h2 pas add def
/h4 h3 pas add def

jaune
[xd h1 xd longueur add h1] ligne
rouge
[xd h2 xd longueur add h2] ligne
bleu
[xd h3 xd longueur add h3] ligne
orange
[xd h4 xd longueur add h4] ligne
noir

#tex# solution exacte
xd longueur add h1 [2 dup] crtexlabel
#tex# Euler d'ordre 1, $h = 0, 05$
xd longueur add h2 [2 dup] crtexlabel
#tex# Euler d'ordre 1, $h = 0, 5$
xd longueur add h3 [2 dup] crtexlabel
#tex# Runge Kutta, $h = 0, 5$
xd longueur add h4 [2 dup] crtexlabel