%%autocrop
20 setxunit
-23 10 setxrange
-6 13 setyrange
%quadrillage marks

/a {-6 4 0} def    
/b {6 4 0} def    
/c {6 -4 0} def    
/d {-6 -4 0} def    
/s {0 0 12} def

/vect_I {-10 cos -10 sin} def
/vect_J {40 cos 40 sin .8 mulv} def
/vect_K {0 1} def

/xyz2xy {
3 dict begin
   /z exch def
   /y exch def
   /x exch def
   vect_I x mulv
   vect_J y mulv
   vect_K z mulv
   addv addv
end
} def

[/A /B /C /D /S] 
[a b c d s] {xyz2xy} capply
mapnp

1.5 S C xdpoint /I defpoint

gsave
   .8 setlinewidth
   pointilles
   [S A B] ligne
   [A D] ligne
grestore

/dotscale {2 dup} def
I times

1.2 setlinewidth
[D C B S] ligne
[S C] ligne
[D S] ligne

%% le plan de base
/P1 {5 -5} def
-9 C D P1 paral xdpoint /P2 defpoint
9 C B P1 paral xdpoint /P3 defpoint
2 setlinewidth
[P2 P1 P3] ligne

12 setfontsize
setTimesItalic
   (A) A ultext   
   (B) B urtext	  
   (C) C drtext	  
   (D) D dltext	  
   (I) I bltext   
   (S) S urtext   

<tex>
\vbox {\hsize 60mm \parindent 0pt
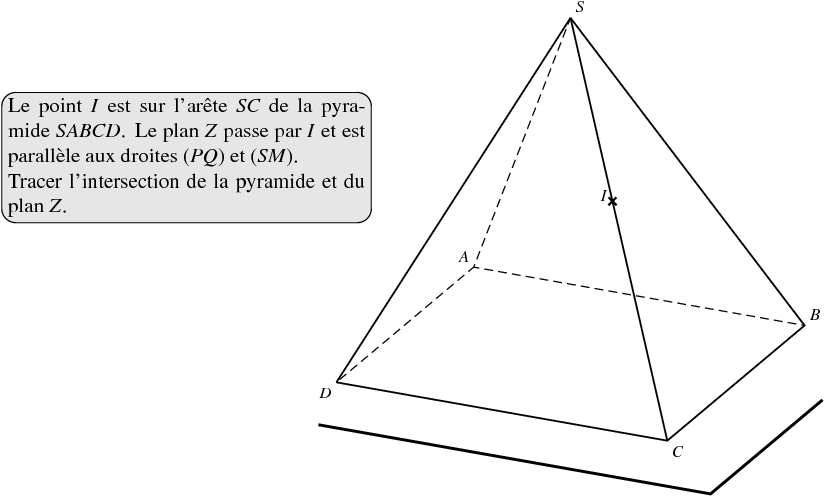
Le point $I$ est sur l'arête $SC$ de la pyramide $SABCD$.
Le plan $Z$ passe par $I$ et est parallèle aux droites $(PQ)$ et
$(SM)$.

Tracer l'intersection de la pyramide et du plan $Z$.
}
</tex>

/fillstyle {.9 setgray fill} def
/linearc .5 store
.8 setlinewidth
/dx_boxit 2 def
/dy_boxit 2 def
boxit
-20.5 4.5 [1.5 dup] urtexlabel