Fichier v_France-Brazil.jps — Modifié le 3 Juillet 2006 à 00 h 12
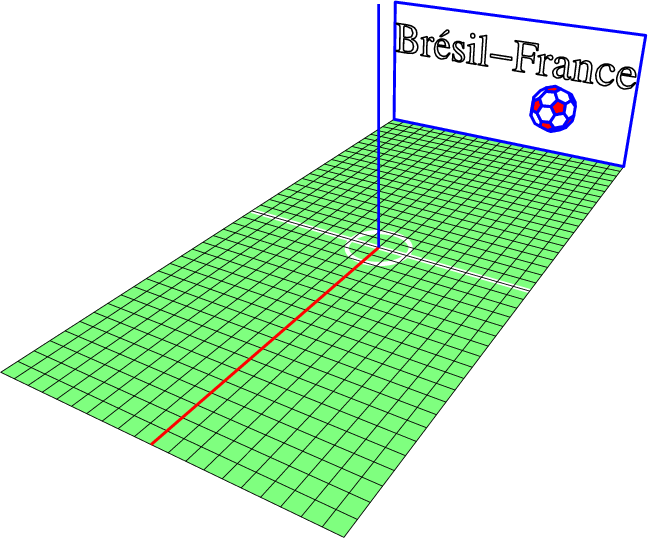
Source
%% Pour passer en pur postscript, decommenter la ligne suivante
%% 294 420 translate
%% puis commenter les 3 suivantes
-15 15 setxrange
-12 12 setyrange
20 setxunit
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Manuel Luque %%
%% juin 2006 %%
%% poour le dessin de l'icosaedre et du ballon %%
%% c'est une adaptation du fichier MatLab de Jean-Bernard ROUX :%%
%% http://hypo.ge-dip.etat-ge.ch/www/math/html/node45.html %%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Pour la mise en perspective%%
%% d'un texte %%
%% Variations autour %%
%% d'un fichier original de %%
%%(c) P. Kleiweg 1997 %%
%% juin 2006 : %%
%% Manuel Luque %%
%% Arnaud Schmittbuhl %%
%% Jean-Paul Vignault %%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
/cm {28.45 mul} def
%% définir le point de vue
%% par ses coordonnées sphériques
/THETA 30 def
/PHI 30 def
/Dobs 50 def % distance observateur
/Decran 20 def % distance de l'écran
%% calcul des coefficients de la matrice
%% de transformation
/Sin1 {THETA sin} bind def
/Sin2 {PHI sin} bind def
/Cos1 {THETA cos} bind def
/Cos2 {PHI cos} bind def
/Cos1Sin2 {Cos1 Sin2 mul} bind def
/Sin1Sin2 {Sin1 Sin2 mul} bind def
/Cos1Cos2 {Cos1 Cos2 mul} bind def
/Sin1Cos2 {Sin1 Cos2 mul} bind def
%%
%% pour la 3D conventionnelle
%% Dony : graphisme scientifique : page 187
%% Editeur : Masson
/XpointVue {Dobs Cos1Cos2 mul} bind def
/YpointVue {Dobs Sin1Cos2 mul} bind def
/ZpointVue {Dobs Sin2 mul} bind def
/3dto2d {
6 dict begin
/Zcote exch def
/Yordonnee exch def
/Xabscisse exch def
/xObservateur Xabscisse Sin1 mul neg Yordonnee Cos1 mul add def
/yObservateur Xabscisse Cos1Sin2 mul neg Yordonnee Sin1Sin2 mul sub Zcote Cos2 mul add def
/zObservateur Xabscisse neg Cos1Cos2 mul Yordonnee Sin1Cos2 mul sub Zcote Sin2 mul sub Dobs add def
%% maintenant on depose les resultats sur la pile
Decran xObservateur mul zObservateur div cm %% c'est Xi cm
Decran yObservateur mul zObservateur div cm %% c'est Yi cm
end
} def
%% les transformations de l'objet
%% translation
/CX -20 def % centre du ballon
/CY 4 def
/CZ 3.5 def
%% rotation autour des axes
/RotX 0 def
/RotY -72 def
/RotZ 144 def
/c2 {RotY cos} bind def
/s2 {RotY sin} bind def
/c3 {RotZ cos} bind def
/s3 {RotZ sin} bind def
/c1 {RotX cos} bind def
/s1 {RotX sin} bind def
%% les coefficients de la matrice de transformation
%% de l'objet
/M11 {c2 c3 mul} bind def
/M12 {c3 s1 mul s2 mul c1 s3 mul sub} bind def
/M13 {c1 c3 mul s2 mul s1 s3 mul add} bind def
/M21 {c2 s3 mul} bind def
/M22 {s1 s2 mul s3 mul c1 c3 mul add} bind def
/M23 {s3 s2 mul c1 mul c3 s1 mul sub} bind def
/M31 {s2 neg} bind def
/M32 {s1 c2 mul} bind def
/M33 {c1 c2 mul} bind def
%%
/CalculsPointsAfterTransformations{%
/Xabscisse M11 Xpoint mul M12 Ypoint mul add M13 Zpoint mul add CX add def
/Yordonnee M21 Xpoint mul M22 Ypoint mul add M23 Zpoint mul add CY add def
/Zcote M31 Xpoint mul M32 Ypoint mul add M33 Zpoint mul add CZ add def
} def
%% le calcul des sommets de l'icosaèdre
/radius 2 def % rayon de la sphère circonscrite
/m 5 def % nombre d'arêtes sur un sommet
/n 3 def % nombre de côtés de chaque face
/sina {180 m div cos 180 n div sin div} bind def
/cosa {1 sina dup mul sub sqrt} bind def
/al {sina cosa atan} bind def
/l {radius 2 mul 180 m div cos mul al cos mul 180 m div sin al sin mul div} bind def
/K {2 radius dup mul mul l dup mul sub 2 radius mul div} bind def
/r {radius dup mul K dup mul sub sqrt} bind def
%% les sommets
%% abscisses
/x1 {r 0 cos mul} bind def
/x2 {r 72 cos mul} bind def
/x3 {r 144 cos mul} bind def
/x4 {r 216 cos mul} bind def
/x5 {r 288 cos mul} bind def
/x6 0 def
/x7 0 def
/x8 {x1 neg} bind def
/x9 {x2 neg} bind def
/x10 {x3 neg} bind def
/x11 {x4 neg} bind def
/x12 {x5 neg} bind def
%% ordonnées
/y1 {r 0 sin mul} bind def
/y2 {r 72 sin mul} bind def
/y3 {r 144 sin mul} bind def
/y4 {r 216 sin mul} bind def
/y5 {r 288 sin mul} bind def
/y6 0 def
/y7 0 def
/y8 {y1 neg} bind def
/y9 {y2 neg} bind def
/y10 {y3 neg} bind def
/y11 {y4 neg} bind def
/y12 {y5 neg} bind def
%% les cotes
/z1 K def
/z2 K def
/z3 K def
/z4 K def
/z5 K def
/z6 radius def
/z7 radius neg def
/z8 K neg def
/z9 K neg def
/z10 K neg def
/z11 K neg def
/z12 K neg def
%% les sommets : 12 sommets = 36 coordonnées
/S [x1 y1 z1 % 0->2
x2 y2 z2 % 3->5
x3 y3 z3 % 6->8
x4 y4 z4 % 9->11
x5 y5 z5 % 12->14
x6 y6 z6 % 15->17
x7 y7 z7 % 18->20
x8 y8 z8 % 21->23
x9 y9 z9 % 24->26
x10 y10 z10 % 27->29
x11 y11 z11 % 30->32
x12 y12 z12 % 33-->35
] def
%% les 20 faces
%% tableau des faces
/FacesIco [ % No
2 6 1 % 0
2 3 6 % 1
6 3 4 % 2
4 5 6 % 3
5 1 6 % 4
1 5 10 % 5
1 10 11 % 6
11 2 1 % 7
11 12 2 % 8
2 12 3 % 9
3 12 8 % 10
8 4 3 % 11
8 9 4 % 12
9 5 4 % 13
5 9 10 % 14
12 11 7 % 15
12 7 8 % 16
9 8 7 % 17
7 10 9 % 18
7 11 10 % 19
] def
%% indice des autres sommets voisins de chaque sommet
/co [ 6 2 11 10 5 % voisins du sommet 1
3 6 1 11 12 % " de 2
2 8 12 4 6 % " de 3
6 5 9 8 3 % " de 4
6 4 10 9 1 % " de 5
1 2 3 4 5 % " de 6
10 9 8 12 11 % " de 7
12 3 4 9 7 % " de 8
8 4 5 10 7 % " de 9
11 7 9 5 1 % " de 10
1 2 12 7 10 % " de 11
11 2 3 8 7 % " de 12
] def
1 setlinejoin
%% Le terrain
newpath
-20 -10 0 3dto2d moveto
-20 10 0 3dto2d lineto
20 10 0 3dto2d lineto
20 -10 0 3dto2d lineto
closepath
gsave
0.5 1 0.5 setrgbcolor
fill
grestore
newpath
2 0 0 3dto2d moveto
0 1 359 { %
/Angle exch def
2 Angle cos mul 2 Angle sin mul 0 3dto2d lineto
} for
closepath
gsave
1 setgray
3 setlinewidth
0 -10 0 3dto2d moveto
0 10 0 3dto2d lineto
stroke
grestore
%% le quadrillage
-20 1 20 {
/x exch def
newpath
x -10 0 3dto2d moveto
x 10 0 3dto2d lineto
0.5 setlinewidth
stroke
} for
-10 1 10 {
/y exch def
newpath
-20 y 0 3dto2d moveto
20 y 0 3dto2d lineto
0.5 setlinewidth
stroke
} for
%% les axes
gsave
%% axe Ox
0 0 moveto
20 0 0 3dto2d lineto
2 setlinewidth
1 0 0 setrgbcolor
stroke
%% axe Oy
% 0 0 moveto
% 0 10 0 3dto2d lineto
% 2 setlinewidth
% 0 1 0 setrgbcolor
% stroke
%% axe Oz
0 0 moveto
0 0 15 3dto2d lineto
2 setlinewidth
0 0 1 setrgbcolor
stroke
grestore
%% dessin de l'icosaedre tronqué
%% paramètre pour tronquer
%% de différentes façons l'icosaèdre
%% 2<d<8 ou plus
/d 3 def % fraction sur l'arete S1S=S1Si/2
/dd {d 1 sub} bind def
/i 0 def
/Sico [ % les coordonnées des sommets de
% l'icosaèdre tronqué
0 5 co length 5 sub {
/j exch def
S i get /xt1 exch def
S i 1 add get /yt1 exch def
S i 2 add get /zt1 exch def
%
co j get 1 sub 3 mul /k exch def
S k get /xt2 exch def
xt1 dd mul xt2 add d div
%
S k 1 add get /yt2 exch def
yt1 dd mul yt2 add d div
%
S k 2 add get /zt2 exch def
zt1 dd mul zt2 add d div
%%
co j 1 add get 1 sub 3 mul /k exch def
S k get /xt2 exch def
xt1 dd mul xt2 add d div
%
S k 1 add get /yt2 exch def
yt1 dd mul yt2 add d div
%
S k 2 add get /zt2 exch def
zt1 dd mul zt2 add d div
%%
co j 2 add get 1 sub 3 mul /k exch def
S k get /xt2 exch def
xt1 dd mul xt2 add d div
%
S k 1 add get /yt2 exch def
yt1 dd mul yt2 add d div
%
S k 2 add get /zt2 exch def
zt1 dd mul zt2 add d div
%%
co j 3 add get 1 sub 3 mul /k exch def
S k get /xt2 exch def
xt1 dd mul xt2 add d div
%
S k 1 add get /yt2 exch def
yt1 dd mul yt2 add d div
%
S k 2 add get /zt2 exch def
zt1 dd mul zt2 add d div
%%
co j 4 add get 1 sub 3 mul /k exch def
S k get /xt2 exch def
xt1 dd mul xt2 add d div
%
S k 1 add get /yt2 exch def
yt1 dd mul yt2 add d div
%
S k 2 add get /zt2 exch def
zt1 dd mul zt2 add d div
/i i 3 add def
} for
] def
%
%% les sommets des faces pentagonales
/FP [ % 12 pentagones
1 5 4 3 2
6 7 8 9 10
15 11 13 12 14
16 17 18 19 20
23 25 21 22 24
26 27 28 29 30
35 31 32 33 34
36 37 38 39 40
41 42 43 44 45
46 50 49 48 47
51 52 53 54 55
56 57 58 59 60 ] def
/FH [ % 20 hexagones
14 15 28 29 16 20
17 16 29 30 21 22
11 15 28 27 7 6
27 26 1 2 8 7
26 30 21 25 5 1
4 5 25 23 49 50
55 51 3 4 50 46
9 8 2 3 51 52
56 57 10 9 52 53
13 11 6 10 57 58
36 37 12 13 58 59
19 20 14 12 37 38
41 42 18 19 38 39
24 22 17 18 42 43
48 49 23 24 43 44
53 54 35 34 60 56
59 60 34 33 40 36
39 40 33 32 45 41
44 45 32 31 47 48
46 47 31 35 54 55] def
/RED 0 def
0 5 FP length 5 sub { % le dessin des pentagones
/i exch def
FP i get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X1 Xabscisse def
/Y1 Yordonnee def
/Z1 Zcote def
%%
FP i 1 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X2 Xabscisse def
/Y2 Yordonnee def
/Z2 Zcote def
%%
FP i 2 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X3 Xabscisse def
/Y3 Yordonnee def
/Z3 Zcote def
%%
FP i 3 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X4 Xabscisse def
/Y4 Yordonnee def
/Z4 Zcote def
%%
FP i 4 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X5 Xabscisse def
/Y5 Yordonnee def
/Z5 Zcote def
%% centre de la face
/xF {X1 X2 add X3 add X4 add X5 add 5 div} bind def
/yF {Y1 Y2 Y3 Y4 Y5 add add add add 5 div} bind def
/zF {Z1 Z2 Z3 Z4 Z5 add add add add 5 div} bind def
%% vecteur : centre de la face -> point de vue
/xV {XpointVue xF sub } bind def
/yV {YpointVue yF sub } bind def
/zV {ZpointVue zF sub } bind def
%% normale
/xN xF CX sub def
/yN yF CY sub def
/zN zF CZ sub def
% le produit scalaire des 2 vecteurs
/PS xV xN mul yV yN mul add zV zN mul add def
PS 0 ge {
newpath
% tracé de la facette
X1 Y1 Z1 3dto2d moveto
X2 Y2 Z2 3dto2d lineto
X3 Y3 Z3 3dto2d lineto
X4 Y4 Z4 3dto2d lineto
X5 Y5 Z5 3dto2d lineto
closepath
gsave
% 0 RED RED 0 setcmykcolor
%% 0 0.5 0.5 0 setcmykcolor
1 0 0 setrgbcolor
fill
grestore
2 setlinewidth
% 0 setgray
0 0 1 setrgbcolor
stroke
} if
/RED RED 0.06 add store
} for
/RED 1 def
0 6 FH length 6 sub { % le dessin des hexagones
/i exch def
FH i get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X1 Xabscisse def
/Y1 Yordonnee def
/Z1 Zcote def
%%
FH i 1 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X2 Xabscisse def
/Y2 Yordonnee def
/Z2 Zcote def
%%
FH i 2 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X3 Xabscisse def
/Y3 Yordonnee def
/Z3 Zcote def
%%
FH i 3 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X4 Xabscisse def
/Y4 Yordonnee def
/Z4 Zcote def
%%
FH i 4 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X5 Xabscisse def
/Y5 Yordonnee def
/Z5 Zcote def
%%
FH i 5 add get 1 sub 3 mul /k exch def
Sico k get /Xpoint exch def
Sico k 1 add get /Ypoint exch def
Sico k 2 add get /Zpoint exch def
CalculsPointsAfterTransformations
/X6 Xabscisse def
/Y6 Yordonnee def
/Z6 Zcote def
%% centre de la face
/xF {X1 X2 add X3 add X4 add X5 add X6 add 6 div} bind def
/yF {Y1 Y2 Y3 Y4 Y5 Y6 add add add add add 6 div} bind def
/zF {Z1 Z2 Z3 Z4 Z5 Z6 add add add add add 6 div} bind def
%% vecteur : centre de la face -> point de vue
/xV {XpointVue xF sub } bind def
/yV {YpointVue yF sub } bind def
/zV {ZpointVue zF sub } bind def
%% normale
/xN xF CX sub def
/yN yF CY sub def
/zN zF CZ sub def
% le produit scalaire des 2 vecteurs
/PS xV xN mul yV yN mul add zV zN mul add def
PS 0 ge {
newpath
% tracé de la facette
X1 Y1 Z1 3dto2d moveto
X2 Y2 Z2 3dto2d lineto
X3 Y3 Z3 3dto2d lineto
X4 Y4 Z4 3dto2d lineto
X5 Y5 Z5 3dto2d lineto
X6 Y6 Z6 3dto2d lineto
closepath
gsave
% 0 0 0.2 0 setcmykcolor
1 setgray
fill
grestore
2 setlinewidth
0 0 1 setrgbcolor
stroke } if
} for
/decalage_vertical 0 def %% decalage en picas du texte en
%% dessous de la ligne y=0
%% Caractères accentués
/ReEncode { exch findfont
dup length dict begin { 1 index /FID eq {pop pop} {def} ifelse
}forall /Encoding ISOLatin1Encoding def currentdict end definefont
pop }bind def
/Font /Times-Roman /ISOfont ReEncode /ISOfont def
Font findfont 3.5 cm scalefont setfont
%% le texte a deformer (les x sont dans [-warphalf ; warphalf])
/warptxt (Brésil-France) def
/warpwidth warptxt stringwidth pop def %% largeur horizontale du texte
/warphalf warpwidth 2 div def %% demi-largeur horizontale
%% Jean-Paul Vignault
%% la procedure de base pour la transformation des points du chemin
%% (x, y) --> (X, Y)
%% cette fonction peut utiliser les variables warpwidth et warphalf
%% point origine de la phrase :
/x0 -20 def
%/y0 -10 def
/y0 warphalf neg 28.45 div def % centre le texte
/z0 6 def
/warp {
3 dict begin
%% /z exch z0 add def
%% /y exch y0 add def
/z exch 28.45 div z0 add def
/y exch 28.45 div y0 add def
x0 y z 3dto2d
end
} bind def
%% pour remplacer 'move'
/warpmove{
%% on teste le booleen place 2 tokens plus en avant sur la pile
%% si c'est 'true', alors on en est au 1er appel => on initialise
%% le chemin
2 index {
newpath
} if
%% puis on applique warp a notre point
warp moveto
%% on enleve le 'true' pour mettre un 'false' a la place
pop false
} bind def
%% pour remplacer 'lineto
/warpline {
warp lineto
} bind def
%% pour remplacer 'curveto'
/warpcurve {
6 2 roll warp
6 2 roll warp
6 2 roll warp
curveto
} bind def
%% 'warpit' declenche la transformation du chemin courant
/warpit {
true
{ warpmove } { warpline } { warpcurve } { closepath } pathforall
pop
} bind def
newpath
%% on se deplace (init chemin) de facon a
%% centrer la ligne de base du texte en (0 , - decalage_vertical)
%%warphalf neg decalage_vertical neg moveto
x0 -10 0 3dto2d moveto
x0 -10 10 3dto2d lineto
x0 10 10 3dto2d lineto
x0 10 0 3dto2d lineto
closepath
0 0 1 setrgbcolor
stroke
0 0 0 3dto2d moveto
warptxt true charpath %% on cree le chemin
%% maintenant on y va
warpit %% on applique le pathforall
gsave
1 setgray
fill
grestore
1 setlinewidth
0 setgray
stroke %% puis on encre
%% showpage