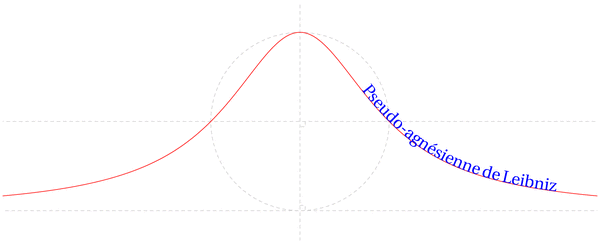
Fichier pseudoleibniz.mp (figure 1) — Modifié le 13 Avril 2008 à 13 h 13
Source
input latexmp;
setupLaTeXMP(class="article",options="12pt",fontencoding="T1",inputencoding="latin1",language="frenchb",packages="fourier,textpathmp");
input textpath;
prologues:=2;
input geometriesyr16;
figure(-10u,-1u,10u,7u);
pair O,A,B,P[],Q[],M[];
O=(0,0);
A-O=u*(3,0);
B=rotation(A,O,90);
path cc,dd;
cc=cercles(B,O);
dd=perpendiculaire(O,B,B);
l=0;
for k=270 step 1 until 629:
if k<>270:
P[k]=pointarc(cc,k);
if (dd intersectiontimes droite(O,P[k]))<>(-1,-1):
Q[k]=dd intersectionpoint droite(O,P[k]);
if (parallele(O,A,P[k]) intersectiontimes parallele(O,B,Q[k]))<>(-1,-1):
l:=l+1;
M[l]=parallele(O,A,P[k]) intersectionpoint parallele(O,B,Q[k]);
fi;
fi;
fi;
endfor;
drawoptions(dashed evenly withcolor gris);
trace cc;trace dd;trace droite(O,B);trace droite(O,A);trace codeperp(B,O,A,5);
trace codeperp(B+A-O,B,O,5);
drawoptions(withcolor rouge);
path pseudo;
pseudo=M1
for k=2 upto l:
--M[k]
endfor;
trace pseudo;
drawoptions(withcolor bleu);
trace textpath("\Large Pseudo-agnésienne de Leibniz",reverse(pseudo),0.57);
fin;
end