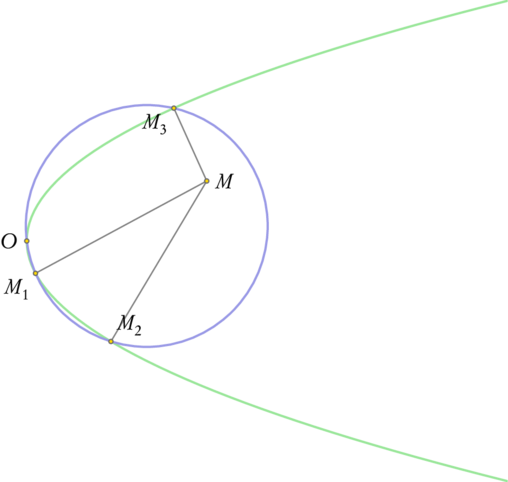
1  Soit P la parabole d'équation y^2=2px et M un point du plan.
  2  Il existe au plus trois normales à P passant par M et au moins une.
  3  Si M_1, M_2 et M_3 sont les trois pieds de ces normales alors les points
  4  M_1, M_2, M_3 et O le sommet de la parabole sont cocycliques.
  5  %@GIAC:
  6  p:=1;
  7  a:=3;
  8  b:=1;
  9  S:=proot(x^3+2*p*(p-a)*x-2*p^2*b);
 10  P:=parabole(y^2=2*p*x);
 11  M:=point(a,b);
 12  O:=point(0);
 13  y:=S[0];M1:=point(y^2/2/p,y);
 14  y:=S[1];M2:=point(y^2/2/p,y);
 15  y:=S[2];M3:=point(y^2/2/p,y);
 16  C:=circonscrit(M1,M2,M3);
 17  segment(M,M1);segment(M,M2);segment(M,M3);
 18  %@STYLE:
 19  global: e=0.6 c=0.5white grille=0 cadre=[-1,-3,5,3]
 20  O: p=lft
 21  P: c=(0.6,0.9,0.6) e=1pt
 22  C: c=(0.6,0.6,0.9) e=1pt
 23  M: p=rt
 24  M1,M3: p=llft