Fichier f01.mp (figure 7) — Modifié le 12 Avril 2008 à 23 h 11
Figures de base pour la géométrie dans l'espace
Source
input couleur;
verbatimtex
%&latex
\documentclass{article}
\usepackage[upright]{fourier}
\begin{document}
etex
beginfig(1);
%representation d'un plan
numeric u;
pair t,r;
transform T,S;
path p;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%on place les points du parallèlogramme représentant le plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
%on trace le parallèlogramme
draw z0--z2;
draw z2--z3;
%on donne un effet d'epaisseur en changeant l'epaisseur du stylo
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
%on rechange l'epaisseur du stylo
pickup pencircle scaled 0.5pt;
%on indique le nom du plan
label.urt(btex $P$ etex, z0+(0.1u,0u));
endfig;
beginfig(2);
%intersection de deux plans
numeric u;
pair t,r;
transform T,S;
path p[],q[];
u= 1cm;
%Tracé de P
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%Tracé de Q
z5 = 0.5[z0,z1];
z6 = z5 transformed S;
z7 = (2.5u,-1u);
z8 = z7 transformed S;
z5 = 0.5[z9,z7];
z10= z9 transformed S;
p1 = z2--z6;
q1= z9--z10;
z11 = p1 intersectionpoint q1;
p2 = z7--z8;
q2= z5--z1;
z12 = p2 intersectionpoint q2;
path pp;
pp=z7--z8--z10--z9--cycle;
fill pp withcolor green;
%fillcolor:=green;
%transparence pp;
path ppp;
ppp:=z5--z6--z11--z9--cycle;
fill ppp withcolor (green+.55*bleu_ciel);
path Pp;
Pp:=z5--z12--z8--z6--cycle;
fill Pp withcolor (green +.75*bleu_ciel);
draw z5--z6 withcolor bleu; %ici on trace la droite d'intersection
draw z9--z7;
draw z9--z10;
draw z10--z6;
draw z6--z3;
draw z6--z8 dashed evenly;
draw z11--z6 dashed evenly;
draw z2--z11;
draw z5--z12 withpen pencircle scaled 2pt;
draw z12--z8 dashed evenly;
draw z7--z12;
label.rt(btex $Q$ etex, z9);
%nom de la droite d'intersection
label.rt(btex $d$ etex, 0.5[z5,z6])withcolor bleu;
endfig;
beginfig(3);
%representation d'un plan defini par trois points
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%tracé du plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%tracé des points
dotlabel.top(btex $A$ etex, (2u,1.5u));
dotlabel.top(btex $B$ etex, (1u,.5u));
dotlabel.top(btex $C$ etex, (3u,1u));
endfig;
beginfig(4);
%representation d'un plan defini par deux droites secantes
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%tracé du plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%tracé des droites
z4 = (0.8u,1u); z5 =(4u,1.5u);draw z4--z5;
z6 = (1u,1.6u);z7=(3.6u,0.4u);draw z6--z7;
label.rt(btex $d$ etex, z5);
label.rt(btex $d'$ etex, z7);
endfig;
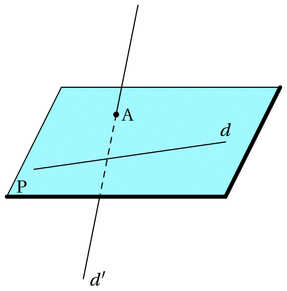
beginfig(5);
%representation d'un plan defini par un point et une droite
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%tracé du plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%le point et la droite
dotlabel.top(btex $A$ etex, (2u,1.5u));
z4 = (1u,.5u);
z5 = (3u,1u);
draw z4--z5;
label.top(btex $d$ etex, z5);
endfig;
beginfig(6);
%representation d'un plan defini par deux droites parallèles
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%tracé du plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%les deux droites
z4 = (1u,1.3u); z5 =(3u,1.8u);draw z4--z5;
z6 = (1.5u,0.2u);z7 = z6 shifted (z5-z4);draw z6--z7;
label.rt(btex $d$ etex, z5);
label.rt(btex $d'$ etex, z7);
endfig;
beginfig(7);
%representation de deux droites non parallelles et sans point commun
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
path p[];
%tracé du plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%tracé de la droite
z4 = (0.5u,.5u);
z5 = (4u,1u);
draw z4--z5;
label.top(btex $d$ etex, z5);
%tracé du point
z6 = (2u,1.5u);
z7 = (0.2u,1u);
dotlabel.rt(btex $A$ etex, z6);
%on met en place les pointillés
z9 = z6 shifted 2z7;
z10 = z6 shifted -3z7;
p1 = z6--z10;
p2 = z0--z1;
z11 = p1 intersectionpoint p2;
draw z6--z11 dashed evenly;
draw z11--z10;
draw z6--z9;
%le nom de la droite
label.rt(btex $d'$ etex, z10);
endfig;
beginfig(8);
%representation d'un plan
numeric u;
pair t,r;
transform T,S;
path p[],q[];
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%Trace de P
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%Trace de Q
z4=(0u,-2.2u);
z5 = z4 transformed T;
z6 = z4 transformed S;
z7 = z4 transformed T transformed S;
path pp;
pp:=z4--z5--z7--z6--cycle;
fill pp withcolor 1.2*green;
draw z4--z6;
pickup pencircle scaled 2pt;
draw z4--z5;
draw z5--z7;
pickup pencircle scaled 0.5pt;
label.urt(btex $Q$ etex, z4+(0.1u,0u));
%Plan d'intersection
z8=1/5[z0,z1]+1/2[z0,z2];
z9=3/5[z4,z5]+1/2[z6,z4];
z10 = z8 transformed S;
z11 = z9 transformed S;
p1 = z10--z11;
q1 = z2--z3;
q2 = z0--z1;
q3 = z6--z7;
z12 = p1 intersectionpoint q1;
z13 = p1 intersectionpoint q2;
z14 = p1 intersectionpoint q3;
p2 = z8--z10;
z15 = p2 intersectionpoint q1;
p3 = z8--z9;
z16 = p3 intersectionpoint q2;
z17 = p3 intersectionpoint q3;
q4 = z4--z5;
z18 = p3 intersectionpoint q4;
p4 = z9--z11;
z19 = p4 intersectionpoint q4;
path k[];
k[1]:=z8--z10--z11--z9--cycle;
fill k[1] withcolor rose;
k[2]:=z8--z15--z12--z16--cycle;
fill k[2] withcolor (.75rose+.15bleu_ciel);
k[3]:=z16--z13--z12--cycle;
fill k[3] withcolor (.75rose+.35bleu_ciel);
k[4]:=z18--z17--z14--z19--cycle;
fill k[4] withcolor (.75rose+.25green);
k[5]:=z18--z19--z11--z14--cycle;
fill k[5] withcolor (.45rose+.45green);
draw z9--z19;draw z19--z11 dashed evenly;
draw z8--z9;
draw z8--z10;
draw z10--z12; draw z12--z13 dashed evenly;draw z13--z14;draw z14--z11 dashed evenly;
draw z2--z15; draw z15--z12 dashed evenly;draw z12--z3;
draw z16--z12;
draw z6--z17;draw z17--z14 dashed evenly;draw z14--z7;
draw z18--z14;
pickup pencircle scaled 2pt;
draw z4--z5;
draw z0--z1;
%nom des droites d'intersection
label.rt(btex $d$ etex, 0.5[z12,z16]);
label.rt(btex $d'$ etex, 0.5[z18,z14]);
endfig;
beginfig(9);
%droite parallele a deux plans secants
numeric u;
pair t,r;
transform T,S;
path p[];
u= 1cm;
t=(4u,1u); r=(0u,2u);
T = identity shifted t;
S = identity shifted r;
%Plan P
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%Plan Q
z4=0.5[z0,z1];
z5 = z4 transformed S;
z6 = z4 shifted (1.5u,-1u);
z4=0.5[z6,z7];
z8 = z6 transformed S;
z9 = z7 transformed S;
p1= z4--z1;
p2 = z6--z8;
z10 = p1 intersectionpoint p2;
p3 = z2--z3; p4 = z9--z7;
z11 = p3 intersectionpoint p4;
path k[];
k[1]:=z8--z9--z7--z6--cycle;
fill k[1] withcolor green;
k[2]:=z11--z5--z4--z7--cycle;
fill k[2] withcolor (.75bleu_ciel+green);
k[3]:=z5--z8--z10--z4--cycle;
fill k[3] withcolor (green+.55bleu_ciel);
draw z5--z11;
draw z11--z9;draw z11--z7 dashed evenly; draw z7--z4 dashed evenly;
label.lft(btex $Q$ etex, z6+(0u,0.5u));
draw z4--z5 withcolor red;
label.lft(btex $\Delta$ etex,0.5[z4,z5])withcolor red;
draw z0--z4;draw z4--z6;draw z6--z8;draw z8--z9;draw z4--z7 dashed evenly;
draw z4--z10 dashed evenly;draw z10--z1;
%droite parallele aux deux plans
z12 = (-1u,0u);
z13 = z12 shifted (0u,3u);
draw z13--z12 withcolor red;
label.lft(btex $d$ etex, z12)withcolor red;
endfig;
beginfig(10);
%theoreme du toit
numeric u;
pair t,r,v;
transform T,S,V;
path p[];
u= 1cm;
t=(3u,2u); r=(-2u,1.5u);v=(-3u,0u);
T = identity shifted t;
S = identity shifted r;
V = identity shifted v;
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed S transformed T;
z4 = z0 transformed V;
z5 = z0 transformed V transformed T;
z101=0.1[z0,z1]; z10=0.9[z0,z1];
z23 = z101 transformed S; z32=z10 transformed S;
z45 = z101 transformed V; z54=z10 transformed V;
p1 = z101--z23; p2 = z4--z5;
z11 = p1 intersectionpoint p2;
path k[];
k[1]:=z45--z54--z32--z23--cycle;
fill k[1] withcolor green;
k[3]:=z23--z101--z10--z32--cycle;
fill k[3] withcolor bleu_ciel;
k[2]:=z23--z32--z54--z11--cycle;
fill k[2] withcolor (.75bleu_ciel+green);
draw z0--z1 ;
draw z2--z3 withcolor red;
%pour un exemple de mise en couleur
draw z101--z23 ; draw z10--z32 ;
draw z23--z45 ; draw z32--z54 dashed evenly ;
draw z4--z11 ;
draw z11--z5 dashed evenly ;
label.rt(btex $d$ etex, z0);
label.rt(btex $d'$ etex, z4);
label.top(btex $\Delta$ etex, z2);
endfig;
beginfig(11);
% plans paralleles a l'aide de droites secantes
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%premier plan P
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%droites secantes
z4 = (0.8u,1u); z5 =(4u,1.5u);draw z4--z5;
z6 = (1u,1.6u);z7=(3.6u,0.4u);draw z6--z7;
label.rt(btex $d$ etex, z5);
label.rt(btex $d'$ etex, z7);
%deuxieme plan Q
z10=(0u,-2.5u);
z11 = z10 transformed T;
z12 = z10 transformed S;
z13 = z10 transformed T transformed S;
path pP;
pP:=z10--z11--z13--z12--cycle;
fill pP withcolor green;
draw z10--z12;
draw z12--z13;
pickup pencircle scaled 2pt;
draw z10--z11;
draw z11--z13;
pickup pencircle scaled 0.5pt;
label.urt(btex $Q$ etex, z10+(0.1u,0u));
%droites secantes
z14 = (0.8u,-1.5u); z15 =(4u,-1u);draw z14--z15;
z16 = (1u,-0.9u);z17=(3.6u,-2.1u);draw z16--z17;
label.rt(btex $d_{1}$ etex, z15);
label.rt(btex $d'_{1}$ etex, z17);
endfig;
beginfig(12);
% parallelisme plan et droite
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%droite dans le plan
z4 = (1u,.5u);
z5 = (4u,1u);
draw z4--z5;
label.top(btex $d'$ etex, z4);
%la droite en dehors du plan
z6 = (1u,2.5u);
z7 = z6 shifted z5-z4;
draw z6--z7;
label.top(btex $d$ etex, z6);
endfig;
beginfig(13);
%droites orthogonales
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(2u,3u); r=(0u,2u);
T = identity shifted t;
S = identity shifted r;
%les droites perpendiculaires en I
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
draw z0--z1;
draw z0--z2;
label.bot(btex $I$ etex, z0);
%marquage de l'angle droit
z3=0.1[z0,z1];z4=0.1[z0,z2];
z5=z3 shifted z4-z0;
draw z3--z5;
draw z4--z5;
%droites d et delta
z6=(0u,-1u);
z7 = z6 transformed T;
draw z7--z6;
label.bot(btex $\Delta$ etex, z7);
z8=(-1u,-1u);
z9= z8 transformed S;
label.lft(btex $d$ etex, z9);
draw z9--z8;
endfig;
beginfig(14);
%droite orthogonale a un plan
numeric u;
pair t,r;
transform T,S;
path p[];
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%plan P
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%droites secantes
z4 = (0.8u,1u); z5 =(4u,1.5u);draw z4--z5;
z6 = (1u,1.6u);z7=(3.6u,0.4u);draw z6--z7;
label.rt(btex $d$ etex, z5);
label.rt(btex $d'$ etex, z7);
p1 = z4--z5;p2 = z6--z7;
%droite orthogonale
z8 = p1 intersectionpoint p2;
z9 = z8 shifted (0u,2u);
label.rt(btex $\Delta$ etex, z9);
draw z8--z9;
z10 = z8 shifted (0u,-2u);
p3 = z9--z10;p4 = z0--z1;
z11 = p3 intersectionpoint p4;
draw z8--z11 dashed evenly;draw z11--z10;
%marquage des angles droits
z12=0.1[z8,z7];z13=0.1[z8,z9];
z14= z13 shifted z12-z8;
draw z12--z14;
draw z13--z14;
z15=0.2[z8,z4];z16=0.1[z8,z9];
z17= z16 shifted z15-z8;
draw z15--z17;
draw z16--z17;
endfig;
beginfig(15);
%plans paralleles et droite orthogonale
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
path p[];
%premier plan et droites
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%droites secantes
z4 = (0.8u,1u); z5 =(4u,1.5u);draw z4--z5;
z6 = (1u,1.6u);z7=(3.6u,0.4u);draw z6--z7;
label.rt(btex $d$ etex, z5);
label.rt(btex $d'$ etex, z7);
%deuxieme plan et droites
z10=(0u,-2.5u);
z11 = z10 transformed T;
z12 = z10 transformed S;
z13 = z10 transformed T transformed S;
path Pp;
Pp:=z10--z11--z13--z12--cycle;
fill Pp withcolor green;
draw z10--z12;
draw z12--z13;
pickup pencircle scaled 2pt;
draw z10--z11;
draw z11--z13;
pickup pencircle scaled 0.5pt;
label.urt(btex $Q$ etex, z10+(0.1u,0u));
%droites secantes
z14 = (0.8u,-1.5u); z15 =(4u,-1u);draw z14--z15;
z16 = (1u,-0.9u);z17=(3.6u,-2.1u);draw z16--z17;
label.rt(btex $d_{1}$ etex, z15);
label.rt(btex $d'_{1}$ etex, z17);
%droite orthogonale
p1=z4--z5;p2=z6--z7;
p3=z14--z15;p4=z16--z17;
p5=z0--z1;p6=z10--z11;
z20 = p1 intersectionpoint p2;
z21 = p3 intersectionpoint p4;
p7 = z20--z21;
z22 = p7 intersectionpoint p5;
z24 = z20 shifted (0u,1.5u);
z25 = z21 shifted (0u,-1.5u);
p8 = z21--z25;
z23 = p8 intersectionpoint p6;
draw z24--z20;draw z20--z22 dashed evenly; draw z22--z21;
draw z21--z23
dashed evenly; draw z23--z25;
label.rt(btex $\Delta$ etex, z24);
%marquage des angles droits
z30=0.2[z20,z4];z31=0.1[z20,z24];
z32 = z31 shifted z30-z20;
draw z32--z30;
draw z32--z31;
z40=0.2[z21,z14];z41=0.1[z21,z22];
z42 = z41 shifted z40-z21;
draw z42--z40;
draw z42--z41;
z50=0.1[z20,z7];z51=0.1[z20,z24];
z52 = z51 shifted z50-z20;
draw z52--z50;
draw z52--z51;
z60=0.1[z21,z17];z61=0.1[z21,z22];
z62 = z61 shifted z60-z21;
draw z62--z60;
draw z62--z61;
endfig;
beginfig(16);
%droites orthogonales a deux plans paralleles
numeric u;
pair t,r;
transform T,S;
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
path p[];
%premier plan
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
path p;
p:=z0--z1--z3--z2--cycle;
fill p withcolor bleu_ciel;
draw z0--z2;
draw z2--z3;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
%deuxieme plan
z10=(0u,-2.5u);
z11 = z10 transformed T;
z12 = z10 transformed S;
z13 = z10 transformed T transformed S;
path pP;
pP:=z10--z11--z13--z12--cycle;
fill pP withcolor green;
draw z10--z12;
draw z12--z13;
pickup pencircle scaled 2pt;
draw z10--z11;
draw z11--z13;
pickup pencircle scaled 0.5pt;
label.urt(btex $Q$ etex, z10+(0.1u,0u));
%premiere droite
z20 = (2u,1u);z26 = z20 shifted (0u,-2.5u);
z21 = z20 shifted (0u,2u);
z22 = z20 shifted (0u,-4.5u);
p1 = z21--z22;
p2 = z0--z1;
p3 = z10--z11;
z24 = p1 intersectionpoint p2;
z25 = p1 intersectionpoint p3;
draw z21--z20;draw z20--z24 dashed evenly;draw z24--z26;draw z26--z25
dashed evenly; draw z25--z22;
%deuxieme droite
z30 = (3u,1.5u);z36 = z30 shifted (0u,-2.5u);
z31 = z30 shifted (0u,2u);
z32 = z30 shifted (0u,-4.5u);
p11 = z31--z32;
p12 = z0--z1;
p13 = z10--z11;
z34 = p11 intersectionpoint p12;
z35 = p11 intersectionpoint p13;
draw z31--z30;draw z30--z34 dashed evenly;draw z34--z36;draw z36--z35
dashed evenly; draw z35--z32;
%marquage des angles droits
z40=0.1[z20,z30];z41=0.1[z20,z21];
z42 = z41 shifted z40-z20;
draw z42--z40;
draw z42--z41;
z50=0.1[z30,z20];z51=0.1[z30,z31];
z52 = z51 shifted z50-z30;
draw z52--z50;
draw z52--z51;
z60=0.1[z26,z36];z61=0.1[z26,z24];
z62 = z61 shifted z60-z26;
draw z62--z60;
draw z62--z61;
z70=0.1[z36,z26];z71=0.2[z36,z34];
z72 = z71 shifted z70-z36;
draw z72--z70;
draw z72--z71;
draw z20--z30;
draw z26--z36;
endfig;
beginfig(17);
%intersection de deux plans perpendiculaires
numeric u;
pair t,r;
transform T,S;
path p[],q[];
u= 1cm;
t=(4u,0u); r=(1u,2u);
T = identity shifted t;
S = identity shifted r;
%Tracé de P
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
draw z0--z2;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
%Tracé de Q
z5 = 0.5[z0,z1];
z6 = z5 transformed S;
z7 = z5 shifted (0u,-2.5u);
z8 = z7 transformed S;
z5 = 0.5[z9,z7];
z10= z9 transformed S;
p1 = z2--z6;
q1= z5--z9;
z11 = p1 intersectionpoint q1;
p2 = z6--z8;
q2= z5--z1;
z12 = p2 intersectionpoint q2;
path k[];
k[1]:=z7--z8--z10--z9--cycle;
fill k[1] withcolor green;
k[3]:=z0--z1--z3--z2--cycle;
fill k[3] withcolor bleu_ciel;
k[2]:=z11--z6--z5--cycle;
fill k[2] withcolor (.55bleu_ciel+green);
k[4]:=z5--z12--z6--cycle;
fill k[4] withcolor (.75bleu_ciel+green);
draw z0--z1--z3 withpen pencircle scaled 2pt;
label.urt(btex $P$ etex, z0+(0.1u,0u));
draw z5--z6 withcolor red;
draw z9--z7;
draw z9--z10;
draw z10--z6;
draw z6--z3;
draw z7--z8;
draw z11--z6 dashed evenly;
draw z2--z11;
draw z12--z6 dashed evenly;
draw z8--z12;
label.rt(btex $Q$ etex, z9);
%nom de la droite d'intersection
label.rt(btex $d$ etex, 0.6[z5,z6])withcolor red;
%droites orthogonales
z13=0.5[z5,z6];
z14 = z13 shifted (0u,2u);
z15 = z13 shifted (0u,-2u);
p3 = z0--z1;
q3 = z13--z15;
z16 = p3 intersectionpoint q3;
draw z14--z13;
draw z13--z16 dashed evenly;
draw z16--z15;
%marquage de l'angle droit
z20=0.2[z13,z6];z21=0.2[z13,z14];
z22 = z21 shifted z20-z13;
draw z22--z20;
draw z22--z21;
z17 = z13 shifted 0.8(z1-z5);
z18 = z13 shifted 0.8(z0-z5);
p4 = z13--z18;
z19 = q1 intersectionpoint p4;
draw z18--z19;
draw z19--z13 dashed evenly;
draw z13--z17;
%marquage de l'angle droit
z30=0.1[z13,z18];z31=0.1[z13,z14];
z32 = z31 shifted z30-z13;
draw z32--z30;
draw z32--z31;
endfig;
beginfig(18);
%plans perpendiculaires a un meme plan
numeric u;
pair t,r;
transform T,S;
path p[],q[];
u= 1cm;
t=(5u,0u); r=(1u,2.3u);
T = identity shifted t;
S = identity shifted r;
%plan Q
z0=(0u,0u);
z1 = z0 transformed T;
z2 = z0 transformed S;
z3 = z0 transformed T transformed S;
%les plans perpendiculaires
z4= 1/4[z0,z1]; z5= 3/4[z0,z1]; z6= 1/2[z4,z5];
z7 = z6 shifted (0u,1u);
z8 = z4 shifted (0u,2u);
z9 = z5 shifted (0u,2u);
z10 = z7 shifted (0u,2u);
z4=0.5[z8,z11];z5=0.5[z12,z9];z7=0.5[z13,z10];
p1 = z2--z3;
q1 = z8--z10;q2=z9--z10;
z14= p1 intersectionpoint q1;
z15= p1 intersectionpoint q2;
z16=1/2[z14,z15];
path k[];
k[1]:=z0--z1--z3--z2--cycle;
fill k[1] withcolor green;
k[3]:=z8--z11--z13--z10--cycle;
fill k[3] withcolor bleu_ciel;
k[2]:=z10--z13--z12--z9--cycle;
fill k[2] withcolor rose;
k[4]:=z8--z14--z16--z7--z4--cycle;
fill k[4] withcolor(green +.75bleu_ciel);
k[5]:=z4--z7--z6--cycle;
fill k[5] withcolor(green+.55bleu_ciel);
k[6]:=z5--z7--z16--z15--z9--cycle;
fill k[6] withcolor(.25green +.75rose);
k[7]:=z5--z7--z6--cycle;
fill k[7] withcolor(.45green+.45rose);
draw z0--z2;
pickup pencircle scaled 2pt;
draw z0--z1;
draw z1--z3;
pickup pencircle scaled 0.5pt;
label.urt(btex $Q$ etex, z0+(0.1u,0u));
draw z4--z7;
draw z5--z7;
draw z8--z11;draw z8--z10;
draw z12--z9;draw z9--z10;
draw z7--z10;
draw z7--z6 dashed evenly;
draw z6--z13;
draw z11--z13; draw z13--z12;
draw z2--z14;draw z14--z15 dashed evenly; draw z15--z3;
%marquage des angles droits;
z20=0.1[z7,z10];z21=0.2[z7,z4];
z22 = z21 shifted z20-z7;
draw z22--z20;
draw z22--z21;
z30=0.1[z7,z10];z31=0.2[z7,z5];
z32 = z31 shifted z30-z7;
draw z32--z30;
draw z32--z31;
label.bot(btex $P$ etex, z11+(0.2u,0.6u));
label.bot(btex $P'$ etex, z12+(-0.2u,0.8u));
endfig;
end