Fichier fg-v8_61-62.mp (figure 1) — Modifié le 4 Avril 2008 à 00 h 23
Construction d'un pentagone
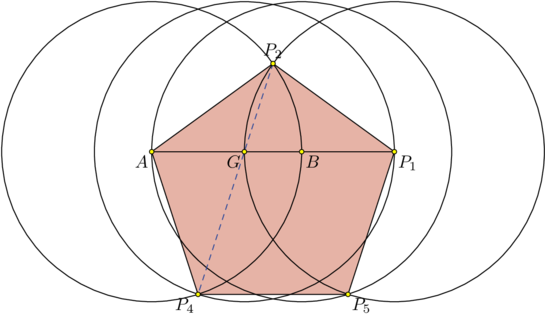
Le point G divise le segment [A,B] selon le nombre d'or.
Quatre cercles de même rayon AB suffisent alors à déterminer les
sommets d'un pentagone.
Source
picture UnBeauPoint;
UnBeauPoint := image(
fill fullcircle scaled 3pt;
fill fullcircle scaled 2pt withcolor red+green;
);
vardef pointe expr p = draw UnBeauPoint shifted p; enddef;
pair A,B,G,P[];
path C[];
UnSurPhi = (sqrt(5) - 1) / 2;
beginfig(1);
A := origin;
B := right scaled 3cm;
G := UnSurPhi [A,B];
C1 := fullcircle scaled (2 abs(B-A)) shifted A;
C2 := C1 shifted (B - A);
C4 := C1 shifted (G - A);
P1 := G + B - A;
C5 := C1 shifted (P1 - A);
P2 := C1 intersectionpoint C5;
P4 := (reverse C1) intersectionpoint C4;
P5 := (reverse C2) intersectionpoint C5;
fill (A--P4--P5--P1--P2--cycle) withcolor (.9,.7,.65);
draw A--P4--P5--P1--P2--cycle;
draw A--P1;
draw C1;
draw C2;
draw C4;
draw C5;
draw P2--P4 dashed evenly
withcolor (0.2,0.3,0.6);
pointe A;
pointe B;
pointe G;
pointe P1;
pointe P2;
pointe P4;
pointe P5;
label.llft(btex $A$ etex, A);
label.llft(btex $G$ etex, G);
label.lrt(btex $B$ etex, B);
label.lrt(btex $P_1$ etex, P1);
label.top(btex $P_2$ etex, P2);
label.llft(btex $P_4$ etex, P4);
label.lrt(btex $P_5$ etex, P5);
endfig;
end