Fichier fig01.mp (figure 1) — Modifié le 2 Juillet 2009 à 15 h 56
Projections et produit vectoriel
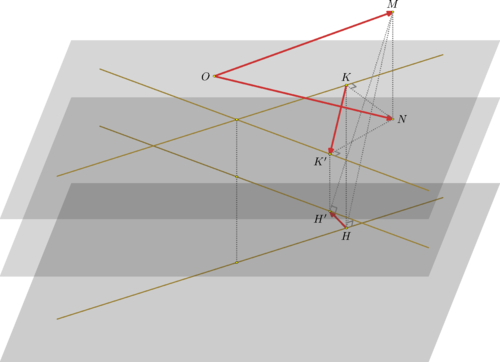
Cette figure est associée à la résolution de l'exercice suivant:

Source
%@AUTEUR: Jean-Michel Sarlat
%@DATE: jeu 02 jui 2009 15:29:38 CEST
input metafun;
% ------------------------------------------------------
% Signe de l'orthogonalité
% ------------------------------------------------------
vardef SigneOrtho(expr a,b,c,x) =
(b + x * unitvector(a - b))
-- (b + x * unitvector(a -b) + x * unitvector(c - b))
-- (b + x * unitvector(c - b))
enddef;
% ------------------------------------------------------
% Pointage
% ------------------------------------------------------
picture UnBeauPoint;
UnBeauPoint := image(
fill fullcircle xscaled 1.7 yscaled 1.4;
fill fullcircle xscaled 1.2 yscaled 0.9 withcolor red+green;
);
vardef pointe expr p = draw UnBeauPoint shifted p; enddef;
% ------------------------------------------------------
% Crayons
% ------------------------------------------------------
def crayonA =
dashed withdots scaled 0.3
withcolor 0.4white
enddef;
def crayonB =
withpen pencircle scaled 1
withcolor (0.8,0.2,0.2)
enddef;
def crayonC =
withpen pencircle scaled 0.5
withcolor 0.5white;
enddef;
% ------------------------------------------------------
% Définitions
% ------------------------------------------------------
numeric u;
u := 1.8cm;
path plan;
plan := ((0,0)--(6,0)--(7,2.5)--(1,2.5)--cycle) scaled u;
path droite[];
droite1 := ((0.8,0.6)--(6.2,2.3)) scaled u;
droite2 := ((1.4,2.1)--(6,0.4)) scaled u;
pair p[];
p1 := droite1 intersectionpoint droite2;
p2 := (5.5u,1.4u);
p3 := point 0.7 of droite2;
p4 := point 0.75 of droite1;
p5 := (3u,2u);
p6 := point 1 of droite2;
p7 := point 1 of droite1;
pair t[];
t1 := (0,1.2u);
t2 := (0,0.8u);
t3 := (0,1.5u);
% ------------------------------------------------------
% Figure
% ------------------------------------------------------
beginfig(1);
fill plan withcolor 0.8*white;
draw droite1 withcolor (0.6,0.5,0.2);
draw SigneOrtho(p2 shifted(t1+t2+t3),p4,p7,4) crayonC;
drawarrow (p4--(p3 shifted t1)) crayonB;
pointe(p1);
pointe(p4);
draw (p1--(p1+t1)) crayonA;
draw (p4--(p4+t1)) crayonA;
fill plan shifted t1 withcolor transparent("normal", 0.2, 0.2*white);
draw droite2 shifted t1 withcolor (0.6,0.5,0.2);
draw SigneOrtho(p2 shifted(t2+t3), p3, p6,4) shifted t1 crayonC;
pointe(p1 shifted t1);
pointe(p3 shifted t1);
draw ((p1+t1)--(p1+t1+t2)) crayonA;
draw ((p3+t1)--(p3+t1+t2)) crayonA;
draw ((p4+t1)--(p4+t1+t2)) crayonA;
fill plan shifted (t1+t2) withcolor transparent("normal", 0.2, 0.2*white);
draw droite1 shifted (t1+t2) withcolor (0.6,0.5,0.2);
draw droite2 shifted (t1+t2) withcolor (0.6,0.5,0.2);
draw SigneOrtho(p6,p3,p2,4) shifted (t1+t2) crayonC;
draw SigneOrtho(p7,p4,p2,4) shifted (t1+t2) crayonC;
drawarrow (p4--p3) shifted (t1+t2) crayonB;
drawarrow (p5--p2) shifted (t1+t2) crayonB;
drawarrow (p5--(p2 shifted t3)) shifted (t1+t2) crayonB;
pointe(p1 shifted (t1+t2));
pointe(p2 shifted (t1+t2));
pointe(p2 shifted (t1+t2+t3));
pointe(p3 shifted (t1+t2));
pointe(p4 shifted (t1+t2));
pointe(p5 shifted (t1+t2));
draw (p2--(p2 shifted t3)) shifted (t1+t2) crayonA;
draw (p2--p3) shifted (t1+t2) crayonA;
draw (p2--p4) shifted (t1+t2) crayonA;
draw ((p2 shifted (t1+t2+t3))--p4) crayonA;
draw ((p2 shifted (t1+t2+t3))--(p3 shifted t1)) crayonA;
label.top(btex $M$ etex scaled 0.8,p2 shifted(t1+t2+t3));
label.bot(btex $H$ etex scaled 0.8,p4);
label.llft(btex $H'$ etex scaled 0.8,p3 shifted(t1));
label.top(btex $K$ etex scaled 0.8,p4 shifted (t1+t2));
label.llft(btex $K'$ etex scaled 0.8,p3 shifted (t1+t2));
label.lft(btex $O$ etex scaled 0.8, p5 shifted (t1+t2));
label.rt(btex $N$ etex scaled 0.8, p2 shifted (t1+t2));
endfig;
end