%@metapost:dijon1996.mp
%@Titre: Dijon -- 1996
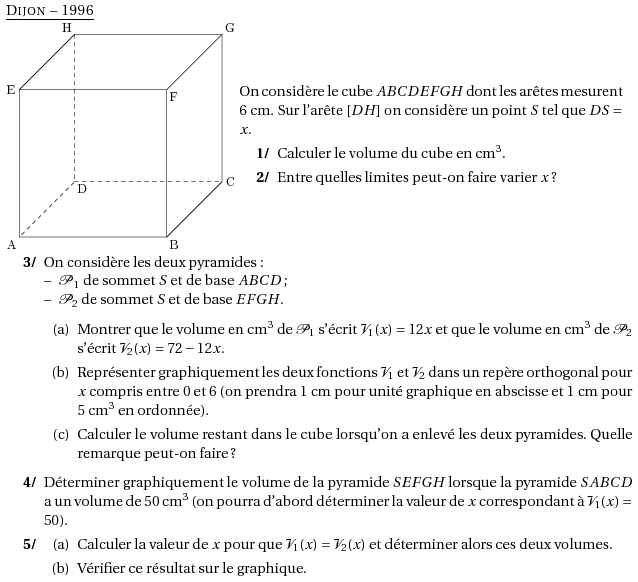
\par\compo{3}{dijon1996}{1}{On considère le cube $ABCDEFGH$ dont les arêtes mesurent 6~cm. Sur l'arête $[DH]$ on considère un point $S$ tel que $DS=x$.
\begin{myenumerate}
\item Calculer le volume du cube en cm$^3$.
\item Entre quelles limites peut-on faire varier $x$?
\end{myenumerate}
}
\begin{myenumerate}
\setcounter{enumi}{2}
\item On considère les deux pyramides :
\begin{itemize}
\item ${\cal P}_1$ de sommet $S$ et de base $ABCD$;
\item ${\cal P}_2$ de sommet $S$ et de base $EFGH$.
\end{itemize}
\begin{enumerate}
\item Montrer que le volume en cm$^3$ de ${\cal P}_1$ s'écrit ${\cal V}_1(x)=12x$ et que le volume en cm$^3$ de ${\cal P}_2$ s'écrit ${\cal V}_2(x)=72-12x$.
\item Représenter graphiquement les deux fonctions ${\cal V}_1$ et ${\cal V}_2$ dans un repère orthogonal pour $x$ compris entre 0 et 6 (on prendra 1~cm pour unité graphique en abscisse et 1~cm pour 5~cm$^3$ en ordonnée).
\item Calculer le volume restant dans le cube lorsqu'on a enlevé les deux pyramides. Quelle remarque peut-on faire ?
\end{enumerate}
\item Déterminer graphiquement le volume de la pyramide $SEFGH$ lorsque la pyramide $SABCD$ a un volume de 50~cm$^3$ (on pourra d'abord déterminer la valeur de $x$ correspondant à ${\cal V}_1(x)=50$).
\item
\begin{enumerate}
\item Calculer la valeur de $x$ pour que ${\cal V}_1(x)={\cal V}_2(x)$ et déterminer alors ces deux volumes.
\item Vérifier ce résultat sur le graphique.
\end{enumerate}
\end{myenumerate}