%@metapost:grenoblesep1999.mp
%@Titre: Grenoble (Sept.) -- 1999
\par\compo{2}{grenoblesep1999}{1}{
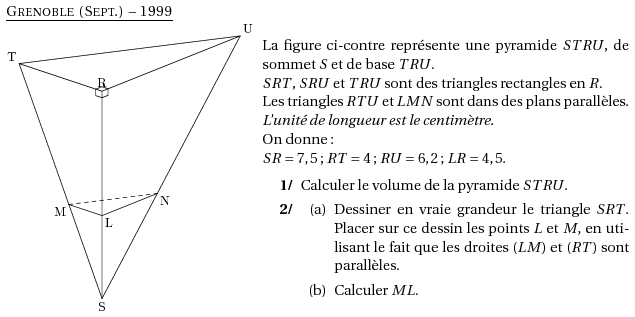
La figure ci-contre représente une pyramide $STRU$, de sommet $S$ et de base $TRU$.

$SRT$, $SRU$ et $TRU$ sont des triangles rectangles en $R$.

Les triangles $RTU$ et $LMN$ sont dans des plans parallèles.

\textit{L'unité de longueur est le centimètre.}

On donne :

$SR=7,5$ ; $RT=4$ ; $RU=6,2$ ; $LR=4,5$.

\begin{myenumerate}
\item Calculer le volume de la pyramide $STRU$.
\item
  \begin{enumerate}
  \item Dessiner en vraie grandeur le triangle $SRT$. Placer sur ce dessin les points $L$ et $M$, en utilisant le fait que les droites $(LM)$ et $(RT)$ sont parallèles.
  \item Calculer $ML$.
  \end{enumerate}
\end{myenumerate}
}