%@metapost:paris2000.mp
%@Titre: Paris -- 2000
\par\compo{4}{paris2000}{1}{
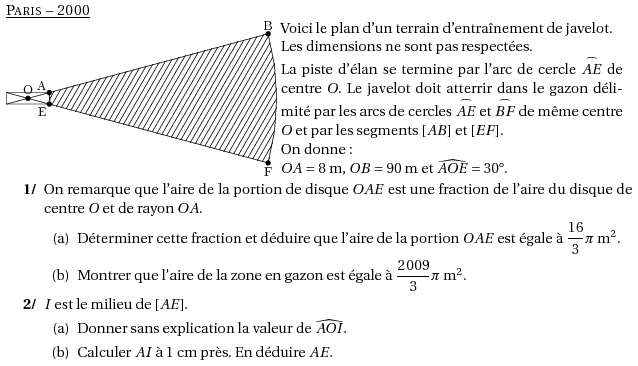
Voici le plan d'un terrain d'entraînement de javelot.

Les dimensions ne sont pas respectées.

La piste d'élan se termine par l'arc de cercle $\stackrel{\frown}{AE}$ de centre $O$. Le javelot doit atterrir dans le gazon délimité par les arcs de cercles $\stackrel{\frown}{AE}$ et $\stackrel{\frown}{BF}$ de même centre $O$ et par les segments $[AB]$ et $[EF]$.

On donne :

$OA=8$~m, $OB=90$~m et $\widehat{AOE}=30$\degres.
}
\begin{myenumerate}
\item On remarque que l'aire de la portion de disque $OAE$ est une fraction de l'aire du disque de centre $O$ et de rayon $OA$.
  \begin{enumerate}
  \item Déterminer cette fraction et déduire que l'aire de la portion $OAE$ est égale à $\dfrac{16}3\pi~\mbox{m}^2$.
  \item Montrer que l'aire de la zone en gazon est égale à $\dfrac{2\,009}3\pi~\mbox{m}^2$.
  \end{enumerate}
\item $I$ est le milieu de $[AE]$.
  \begin{enumerate}
  \item Donner sans explication la valeur de $\widehat{AOI}$.
  \item Calculer $AI$ à 1~cm près. En déduire $AE$.
  \end{enumerate}
\end{myenumerate}