%@metapost:nordsep2000.mp
%@Titre: Nord (Sept.) -- 2000
\par\compo{4}{nordsep2000}{1}{
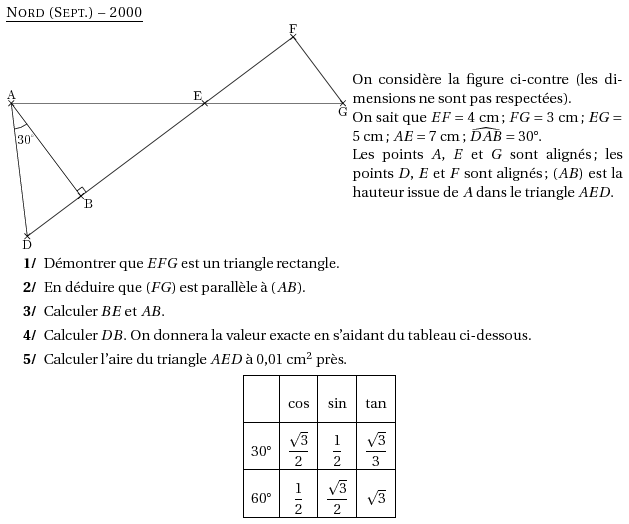
On considère la figure ci-contre (les dimensions ne sont pas respectées).
\\On sait que $EF=4$~cm ; $FG=3$~cm ; $EG=5$~cm ; $AE=7$~cm ; $\widehat{DAB}=30$\degres.
\\Les points $A$, $E$ et $G$ sont alignés ; les points $D$, $E$ et $F$ sont alignés ; $(AB)$ est la hauteur issue de $A$ dans le triangle $AED$.
}
\begin{myenumerate}
\item Démontrer que $EFG$ est un triangle rectangle.
\item En déduire que $(FG)$ est parallèle à $(AB)$.
\item Calculer $BE$ et $AB$.
\item Calculer $DB$. On donnera la valeur exacte en s'aidant du tableau ci-dessous.
\item Calculer l'aire du triangle $AED$ à 0,01~cm$^2$ près.
\end{myenumerate}
$$
\renewcommand{\arraystretch}{2.5}
\begin{tabular}{|c|c|c|c|}
\hline
&$\cos$&$\sin$&$\tan$\\
\hline
30\degres&$\dfrac{\sqrt3}2$&$\dfrac12$&$\dfrac{\sqrt3}3$\\
\hline
60\degres&$\dfrac12$&$\dfrac{\sqrt3}2$&$\sqrt3$\\
\hline
\end{tabular}
\renewcommand{\arraystretch}{1}
$$