%@metapost:europe2000.mp
%@Titre: Europe -- 2000
\par\compo{6}{europe2000}{1}{
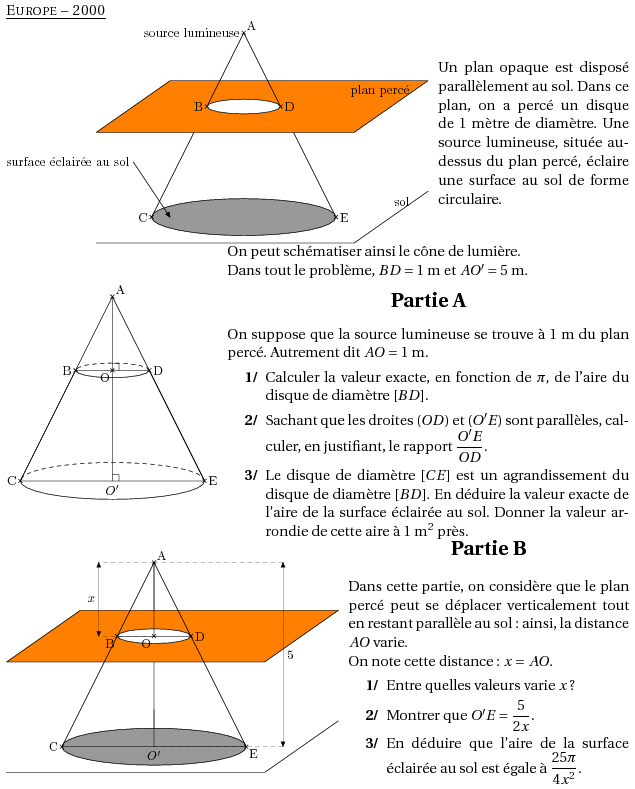
Un plan opaque est disposé parallèlement au sol. Dans ce plan, on a percé un disque de 1 mètre de diamètre. Une source lumineuse, située au-dessus du plan percé, éclaire une surface au sol de forme circulaire.
}
\par\compo{7}{europe2000}{1}{On peut schématiser ainsi le cône de lumière.
\\Dans tout le problème, $BD=1$~m et $AO'=5$~m.
\begin{center}
\textbf{\Large{Partie A }}
\end{center}
On suppose que la source lumineuse se trouve à 1~m du plan percé. Autrement dit $AO=1$~m.
\begin{myenumerate}
\item Calculer la valeur exacte, en fonction de $\pi$, de l'aire du disque de diamètre $[BD]$.
\item Sachant que les droites $(OD)$ et $(O'E)$ sont parallèles, calculer, en justifiant, le rapport $\dfrac{O'E}{OD}$.
\item Le disque de diamètre $[CE]$ est un agrandissement du disque de diamètre $[BD]$. En déduire la valeur exacte de l'aire de la surface éclairée au sol. Donner la valeur arrondie de cette aire à 1~m$^2$ près.
\end{myenumerate}
}
\par\compo{8}{europe2000}{1}{
\begin{center}
\textbf{\Large{Partie B }}
\end{center}
Dans cette partie, on considère que le plan percé peut se déplacer verticalement tout en restant parallèle au sol : ainsi, la distance $AO$ varie.
\\On note cette distance : $x=AO$.
\begin{myenumerate}
\item Entre quelles valeurs varie $x$ ?
\item Montrer que $O'E=\dfrac5{2x}$.
\item En déduire que l'aire de la surface éclairée au sol est égale à $\dfrac{25 \pi}{4x^2}$.
\end{myenumerate}
}