Modifié le 27 Octobre 2006 à 21 h 12.
Source
%@metapost:est2001.mp
%@Titre: Groupe Est -- 2001
\par\compo{3}{est2001}{1}{
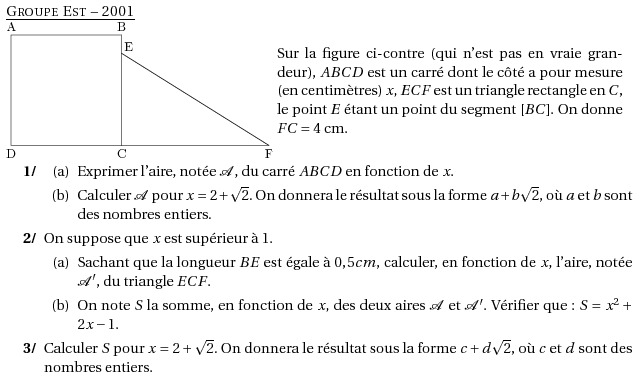
Sur la figure ci-contre (qui n'est pas en vraie grandeur), $ABCD$ est
un carré dont le côté a pour mesure (en centimètres) $x$, $ECF$ est un
triangle rectangle en $C$, le point $E$ étant un point du segment
$[BC]$. On donne $FC=4$~cm.
}
\begin{myenumerate}
\item
\begin{enumerate}
\item Exprimer l'aire, notée $\cal{A}$, du carré $ABCD$ en fonction
de $x$.
\item Calculer $\cal{A}$ pour $x=2+\sqrt2$. On donnera le résultat
sous la forme $a+b\sqrt2$, où $a$ et $b$ sont des nombres entiers.
\end{enumerate}
\item On suppose que $x$ est supérieur à 1.
\begin{enumerate}
\item Sachant que la longueur $BE$ est égale à $0,5cm$, calculer, en
fonction de $x$, l'aire, notée $\cal{A}'$, du triangle $ECF$.
\item On note $S$ la somme, en fonction de $x$, des deux aires
$\cal{A}$ et $\cal{A}'$. Vérifier que : $S=x^2+2x-1$.
\end{enumerate}
\item Calculer $S$ pour $x=2+\sqrt2$. On donnera le résultat sous la
forme $c+d\sqrt2$, où $c$ et $d$ sont des nombres entiers.
\end{myenumerate}