%@metapost:est2001.mp
%@Titre: Groupe Est -- 2001
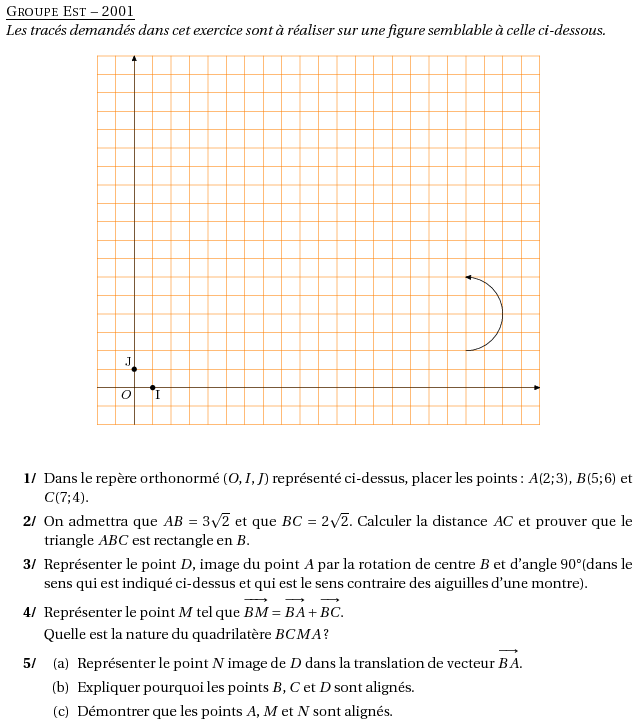
\par\textit{Les tracés demandés dans cet exercice sont à réaliser sur une figure semblable à celle ci-dessous.}
$$\includegraphics{est2001.4}$$
\begin{myenumerate}
\item Dans le repère orthonormé $(O, I, J)$ représenté ci-dessus,
  placer les points : $A(2 ; 3)$, $B(5 ; 6)$ et $C(7 ; 4)$.
\item On admettra que $AB=3\sqrt2$ et que $BC=2\sqrt2$. Calculer la
  distance $AC$ et prouver que le triangle $ABC$ est rectangle en $B$.
\item Représenter le point $D$, image du point $A$ par la rotation de
  centre $B$ et d'angle 90\degres (dans le sens qui est indiqué
  ci-dessus et qui est le sens contraire des aiguilles d'une montre).
\item Représenter le point $M$ tel que $\vecteur{BM}=\vecteur{BA}+\vecteur{BC}$.

Quelle est la nature du quadrilatère $BCMA$ ?
\item
\begin{enumerate}
\item Représenter le point $N$ image de $D$ dans la translation de vecteur $\vecteur{BA}$.
\item Expliquer pourquoi les points $B$, $C$ et $D$ sont alignés.
\item Démontrer que les points $A$, $M$ et $N$ sont alignés.
\end{enumerate}
\end{myenumerate}