Modifié le 27 Octobre 2006 à 21 h 14.
Source
%@metapost:reunion2001.mp
%@Titre: Réunion -- 2001
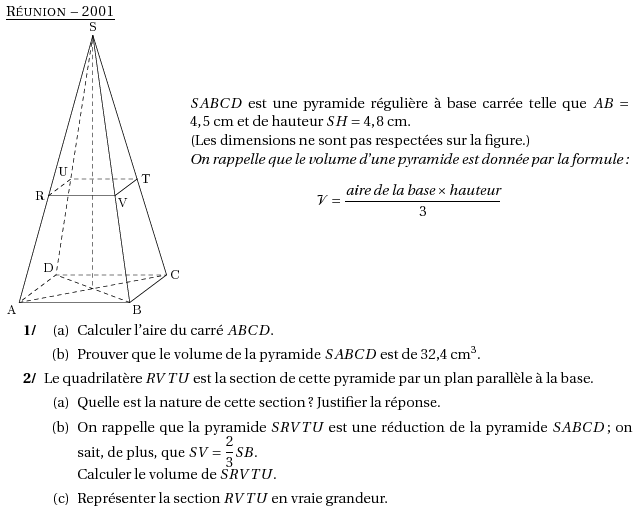
\par\compo{2}{reunion2001}{1}{$SABCD$ est une pyramide régulière à
base carrée telle que $AB=4,5$~cm et de hauteur $SH=4,8$~cm.\\(Les
dimensions ne sont pas respectées sur la figure.)\\{\em On rappelle
que le volume d'une pyramide est donnée par la formule:
$${\cal V}=\frac{\mbox{aire de la base}\times\mbox{hauteur}}3$$
}}
\par\begin{myenumerate}
\item
\begin{enumerate}
\item Calculer l'aire du carré $ABCD$.
\item Prouver que le volume de la pyramide $SABCD$ est de 32,4~cm$^3$.
\end{enumerate}
\item Le quadrilatère $RVTU$ est la section de cette pyramide par un
plan parallèle à la base.
\begin{enumerate}
\item Quelle est la nature de cette section ? Justifier la réponse.
\item On rappelle que la pyramide $SRVTU$ est une réduction de la
pyramide $SABCD$; on sait, de plus, que $SV=\dfrac23SB$.\\Calculer
le volume de $SRVTU$.
\item Représenter la section $RVTU$ en vraie grandeur.
\end{enumerate}
\end{myenumerate}