%@metapost:sud2001.mp
%@Titre: Groupe Sud -- 2001
\begin{center}
\textbf{\Large{Partie I}}
\end{center}
\compo{1}{sud2001}{1}{
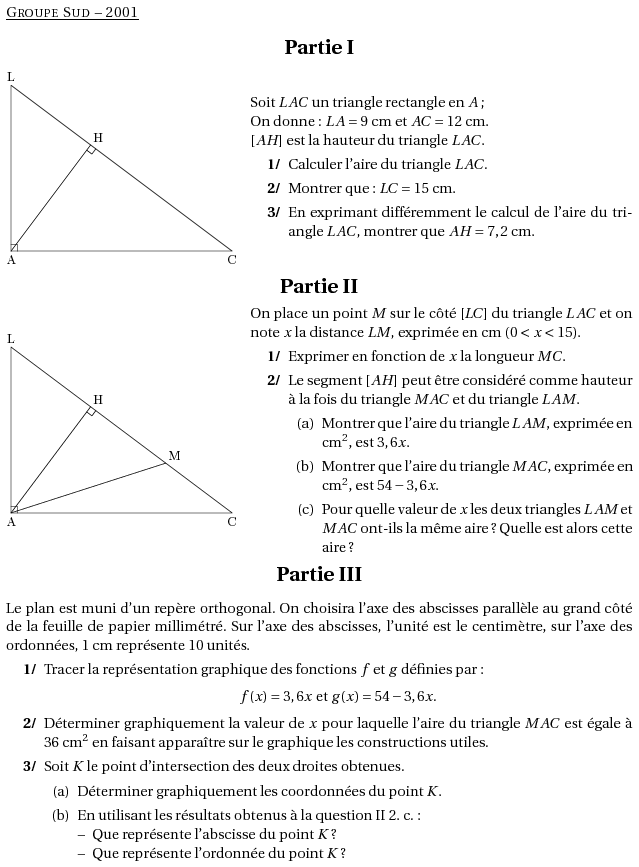
Soit $LAC$ un triangle rectangle en $A$;

On donne : $LA=9$~cm et $AC=12$~cm.

$[AH]$ est la hauteur du triangle $LAC$.
\begin{myenumerate}
\item Calculer l'aire du triangle $LAC$.
\item Montrer que : $LC=15$~cm.
\item En exprimant différemment le calcul de l'aire du triangle $LAC$, montrer que $AH=7,2$~cm.
\end{myenumerate}
}
\begin{center}
\textbf{\Large{Partie II}}
\end{center}
\compo{2}{sud2001}{1}
{
On place un point $M$ sur le côté $[LC]$ du triangle $LAC$ et on note $x$ la distance $LM$, exprimée en cm ($0<x<15$).
\begin{myenumerate}
\item Exprimer en fonction de $x$ la longueur $MC$.
\item Le segment $[AH]$ peut être considéré comme hauteur à la fois du triangle $MAC$ et du triangle $LAM$.
\begin{enumerate}
\item Montrer que l'aire du triangle $LAM$, exprimée en cm$^2$, est $3,6x$.
\item Montrer que l'aire du triangle $MAC$, exprimée en cm$^2$, est $54-3,6x$.
\item Pour quelle valeur de $x$ les deux triangles $LAM$ et $MAC$ ont-ils la même aire ? Quelle est alors cette aire ?
\end{enumerate}
\end{myenumerate}
}
\begin{center}
\textbf{\Large{Partie III}}
\end{center}
Le plan est muni d'un repère orthogonal. On choisira l'axe des abscisses parallèle au grand côté de la feuille de papier millimétré. Sur l'axe des abscisses, l'unité est le centimètre, sur l'axe des ordonnées, 1~cm représente 10 unités.
\begin{myenumerate}
\item Tracer la représentation graphique des fonctions $f$ et $g$ définies par :
\begin{center}
$f(x)=3,6x$ et $g(x)=54-3,6x$.
\end{center}
\item Déterminer graphiquement la valeur de $x$ pour laquelle l'aire du triangle $MAC$ est égale à 36~cm$^2$ en faisant apparaître sur le graphique les constructions utiles.
\item Soit $K$ le point d'intersection des deux droites obtenues.
\begin{enumerate}
\item Déterminer graphiquement les coordonnées du point $K$.
\item En utilisant les résultats obtenus à la question II 2. c. :
\begin{itemize}
\item Que représente l'abscisse du point $K$ ?
\item Que représente l'ordonnée du point $K$ ?
\end{itemize}
\end{enumerate}
\end{myenumerate}