%@metapost:sud2003.mp
%@Titre: Groupe Sud -- 2003
\compo{4}{sud2003}{1}{
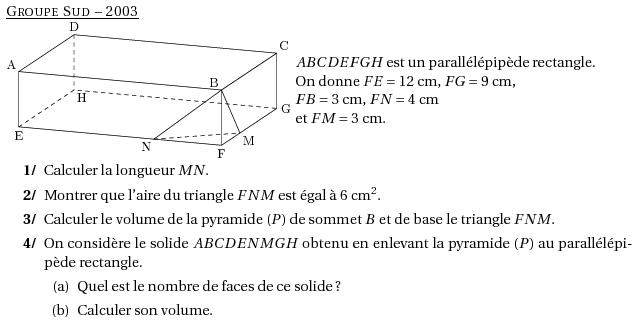
$ABCDEFGH$ est un parallélépipède rectangle.

On donne $FE=12$~cm, $FG=9$~cm,

$FB=3$~cm, $FN=4$~cm

et $FM=3$~cm.
}
\begin{myenumerate}
\item Calculer la longueur $MN$.
\item Montrer que l'aire du triangle $FNM$ est égal à 6~cm$^2$.
\item Calculer le volume de la pyramide $(P)$ de sommet $B$ et de base le triangle $FNM$.
\item On considère le solide $ABCDENMGH$ obtenu en enlevant la pyramide $(P)$ au parallélépipède rectangle.
\begin{enumerate}
\item Quel est le nombre de faces de ce solide ?
\item Calculer son volume.
\end{enumerate} 
\end{myenumerate}