%@metapost:Metropole2009.mp
%@Titre:Métropole -- 2009
On considère un tiangle $ABC$ tel que $AB=17,5$~cm; $BC=14$~cm; $AC=10,5$~cm.
\paragraph{Partie 1}\hfill\newline
\begin{myenumerate}
\item Démontrer que le triangle $ABC$ est rectangle en $C$.
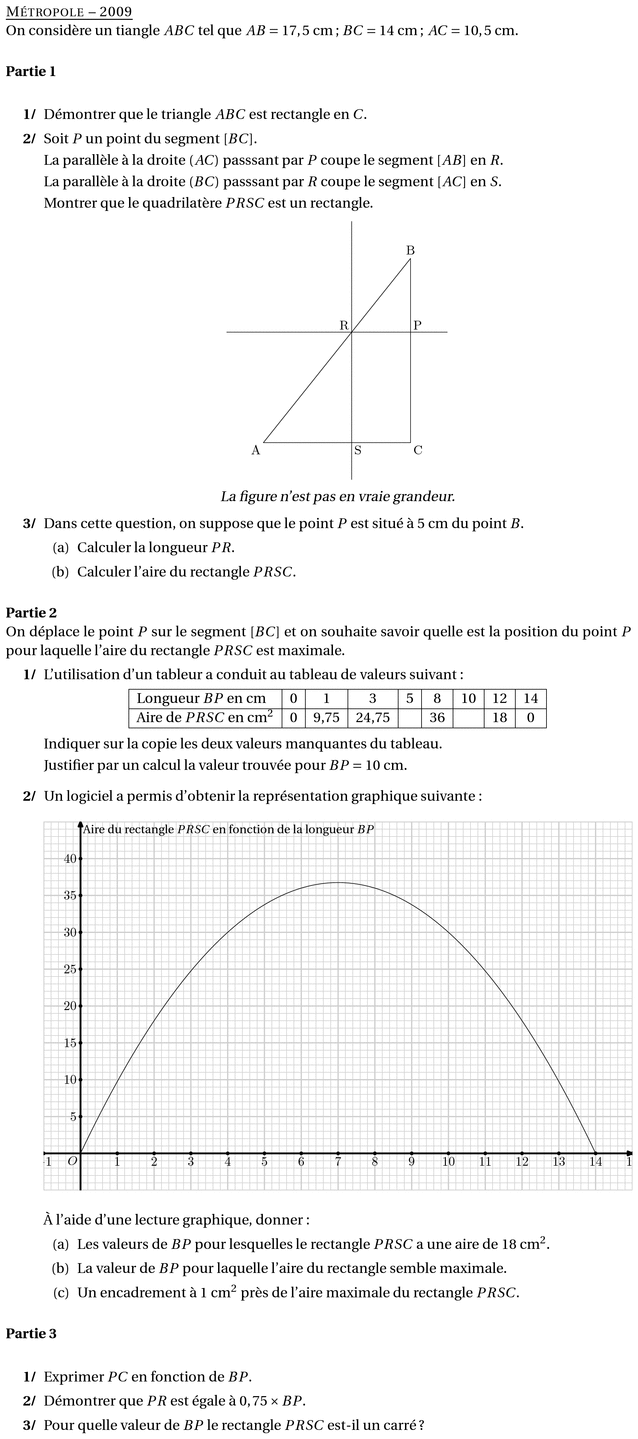
\item Soit $P$ un point du segment $[BC]$.\par
  La parallèle à la droite $(AC)$ passsant par $P$ coupe le segment $[AB]$
  en $R$.\par
  La parallèle à la droite $(BC)$ passsant par $R$ coupe le segment $[AC]$
  en $S$.\par
  Montrer que le quadrilatère $PRSC$ est un rectangle.
  \begin{center}
    \includegraphics{Metropole2009.2}\par
    {\sl La figure n'est pas en vraie grandeur.}
  \end{center}
\item Dans cette question, on suppose que le point $P$ est situé à
  5~cm du point $B$.
  \begin{enumerate}
  \item Calculer la longueur $PR$.
  \item Calculer l'aire du rectangle $PRSC$.
  \end{enumerate}
\end{myenumerate}
\paragraph{Partie 2}\hfill\newline
On déplace le point $P$ sur le segment $[BC]$ et on souhaite savoir quelle
est la position du point $P$ pour laquelle l'aire du rectangle $PRSC$ est
maximale.
\begin{myenumerate}
\item L'utilisation d'un tableur a conduit au tableau de valeurs
  suivant :
  \begin{center}
    \begin{tabular}{|l|*{8}{c|}}
      \hline
      Longueur $BP$ en cm &
      \hfil0 & \hfil1 & \hfil3 & \hfil5 & \hfil8 & \hfil10 & 
      \hfil12 & \hfil14\\\hline
      Aire de $PRSC$ en cm$^2$ &
      \hfil0 & \hfil9,75 & \hfil24,75 &  & \hfil36 & & 
      \hfil18 & \hfil0\\\hline
    \end{tabular}
  \end{center}
  Indiquer sur la copie les deux valeurs manquantes du tableau.\par
  Justifier par un calcul la valeur trouvée pour
  $BP=10$~cm.
\item Un logiciel a permis d'obtenir la représentation graphique
  suivante :
  \[\includegraphics{Metropole2009courbe.2}\]
  \`A l'aide d'une lecture graphique, donner :
  \begin{enumerate}
  \item Les valeurs de $BP$ pour lesquelles le rectangle $PRSC$ a une
    aire de 18~cm$^2$.
  \item La valeur de $BP$ pour laquelle l'aire du rectangle semble
    maximale.
  \item Un encadrement à 1~cm$^2$ près de l'aire maximale
    du rectangle $PRSC$.
  \end{enumerate}
\end{myenumerate}
\paragraph{Partie 3}\hfill\newline
\begin{myenumerate}
\item Exprimer $PC$ en fonction de $BP$.
\item Démontrer que $PR$ est égale à $0,75\times BP$.
\item Pour quelle valeur de $BP$ le rectangle $PRSC$ est-il un carré ?
\end{myenumerate}