%@metapost:Liban2009courbe.mp
%@Titre: Liban -- 2009
\begin{center}
\textbf{Les trois parties sont indépendantes}
\end{center}

Deux frères ont hérité d'un terrain que l'on peut assimiler à un
triangle rectangle.\\
L'aire de ce terrain est égale à \nombre{2400}~m$^2$.

Ils désirent construire un muret afin de partager ce terrain en deux
parcelles de même aire, soit \nombre{1200}~m$^2$ par parcelle.

Pour cela, on partage le terrain selon un segment $[MN]$, $M$ et $N$
étant respectivement sur les côtés $[CB]$ et $[CA]$. Les droites
$(MN)$ et $(AB)$ sont parallèles.

Dans tout ce problème, l'unité de longueur est le mètre. On donne :
$AB=60$ et $BC=80$.

\medskip

\textbf{Partie A}\\

\compog{1}{Liban2009}{1}{%
Dans cette partie : $CM=50$.
\begin{myenumerate}
\item Justifier que $MN=37,5$.
\item Comparer les aires du triangle $CMN$ et du trapèze $ANMB$ après
  les avoir calculées.
\item Pour que les deux aires soient égales, doit-on placer le point
  $M$ à plus de 50 m de $C$ ou à moins de 50 m de $C$ ?
\end{myenumerate}
}
\medskip

\textbf{Partie B}
 
\compog{2}{Liban2009}{1}{%
On veut déterminer la distance $CM$ pour laquelle l'aire du triangle
$CNM$ est égale à \nombre{1200}~m$^2$.
 
On pose $CM=x$.

\begin{myenumerate}
\item Démontrer que $MN=\dfrac{3}{4}x$.
\item Démontrer que l'aire du triangle $CNM$, exprimée en m\up{2}, a
  pour mesure : $\dfrac{3}{8}x^2$.
\end{myenumerate}
}
\begin{myenumerate}
\setcounter{enumi}{2}
\item Soit $f$ la fonction qui, au nombre $x$ appartenant à
  l'intervalle $[0\,;\,80]$, associe l'aire du triangle $CMN$.\\
On note $f : x \longmapsto \dfrac{3}{8}x^2$.
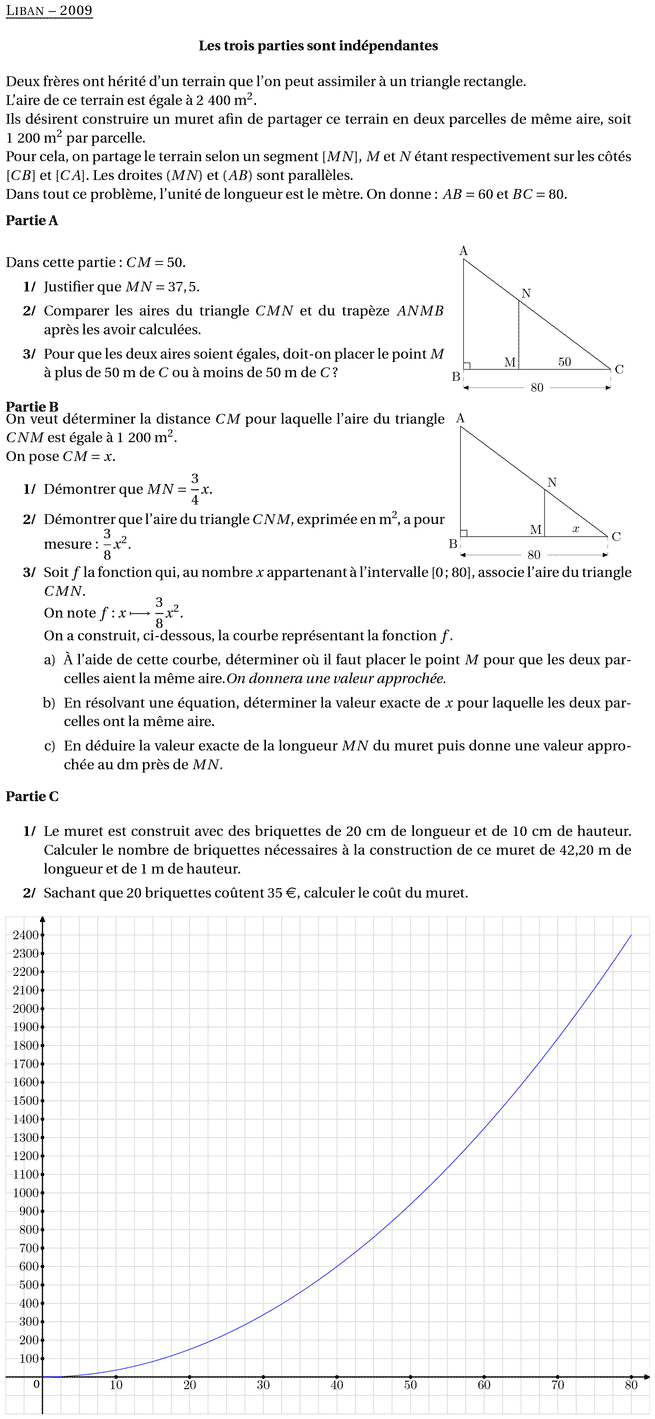
\\On a construit, ci-dessous, la courbe représentant la fonction $f$.
\begin{enumerate}[a)]
\item\`A l'aide de cette courbe, déterminer où il faut placer le point
  $M$ pour que les deux parcelles aient la même aire.\emph{On donnera
    une valeur approchée.}
\item En résolvant une équation, déterminer la valeur exacte de $x$
  pour laquelle les deux parcelles ont la même aire.
\item En déduire la valeur exacte de la longueur $MN$ du muret puis
  donne une valeur approchée au dm près de $MN$.
\end{enumerate}
\end{myenumerate}

\medskip

\textbf{Partie C}
 
\medskip

\begin{myenumerate}
\item Le muret est construit avec des briquettes de 20~cm de longueur
  et de 10~cm de hauteur. Calculer le nombre de briquettes nécessaires
  à la construction de ce muret de 42,20~m  de longueur et de 1~m  de
  hauteur.
\item Sachant que 20~briquettes coûtent 35~\eurologo, calculer le coût
  du muret.
\end{myenumerate}
\[\includegraphics{Liban2009courbe.1}\]