%@P:exocorcp
%@metapost:diveucl605exo008.mp
\par\dispo{1}{
  \begin{tabular}{|c|m{1.5cm}|m{1.5cm}|m{1.5cm}|}
    \cline{2-4}
\multicolumn{1}{c|}{}&Multiple de 2&Multiple de 4&Multiple de 5\\
\hline
0&&&\\
\hline
1&&&\\
\hline
2&&&\\
\hline
3&&&\\
\hline
4&&&\\
\hline
5&&&\\
\hline
6&&&\\
\hline
7&&&\\
\hline
8&&&\\
\hline
9&&&\\
\hline
10&&&\\
\hline
11&&&\\
\hline
12&&&\\
\hline
13&&&\\
\hline
14&&&\\
\hline
15&&&\\
\hline
16&&&\\
\hline
  \end{tabular}
}{
\[\includegraphics{diveucl605exo008.1}\]
}
\begin{myenumerate}
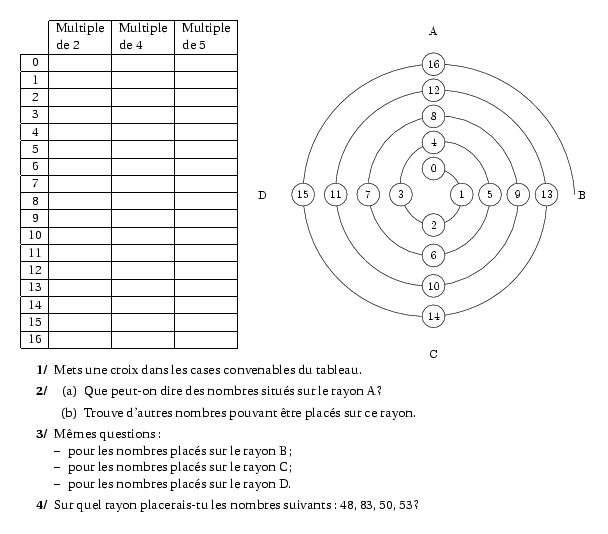
  \item Mets une croix dans les cases convenables du tableau.
  \item
    \begin{enumerate}
    \item Que peut-on dire des nombres situés sur le rayon A ?
    \item Trouve d'autres nombres pouvant être placés sur ce rayon.
    \end{enumerate}
  \item Mêmes questions :
    \begin{itemize}
      \item pour les nombres placés sur le rayon B ;
      \item pour les nombres placés sur le rayon C ;
      \item pour les nombres placés sur le rayon D.
    \end{itemize}
  \item Sur quel rayon placerais-tu les nombres suivants : 48, 83, 50, 53 ?
\end{myenumerate}
%@Correction:
\dispo{1}{
  \begin{tabular}{|c|m{1.5cm}|m{1.5cm}|m{1.5cm}|}
    \cline{2-4}
\multicolumn{1}{c|}{}&Multiple de 2&Multiple de 4&Multiple de 5\\
\hline
0&\ding{56}&\ding{56}&\ding{56}\\
\hline
1&&&\\
\hline
2&\ding{56}&&\\
\hline
3&&&\\
\hline
4&\ding{56}&\ding{56}&\\
\hline
5&&&\ding{56}\\
\hline
6&\ding{56}&&\\
\hline
7&&&\\
\hline
8&\ding{56}&\ding{56}&\\
\hline
9&&&\\
\hline
10&\ding{56}&&\ding{56}\\
\hline
11&&&\\
\hline
12&\ding{56}&\ding{56}&\\
\hline
13&&&\\
\hline
14&\ding{56}&&\\
\hline
15&&&\ding{56}\\
\hline
16&\ding{56}&\ding{56}&\\
\hline
  \end{tabular}
}{
\begin{myenumerate}
  \setcounter{enumi}{1}
  \item
    \begin{enumerate}
    \item Ce sont tous des multiples de 4.
    \item 20; 24; 28; \ldots
    \end{enumerate}
  \item 
    \begin{itemize}
      \item Ce sont des multiples de 4 plus 1. On peut choisir 21; 25; 29; \ldots
      \item Ce sont des multiples de 4 plus 2. On peut choisir 22; 26; 30; \ldots
      \item Ce sont des multiples de 4 plus 3. On peut choisir 23; 28; 31; \ldots
    \end{itemize}
  \item 48 est un multiple de 4 : sur le rayon A. \opidiv[style=text]{83}{4} donc sur le rayon D. \opidiv[style=text]{50}{4} donc sur le rayon C. \opidiv[style=text]{53}{4} donc sur le rayon B.
\end{myenumerate}
}