Modifié le 3 Mai 2009 à 21 h 01.
Source
%@metapost: 603actiquoeg.mp
%@Dif:2
\begin{myenumerate}
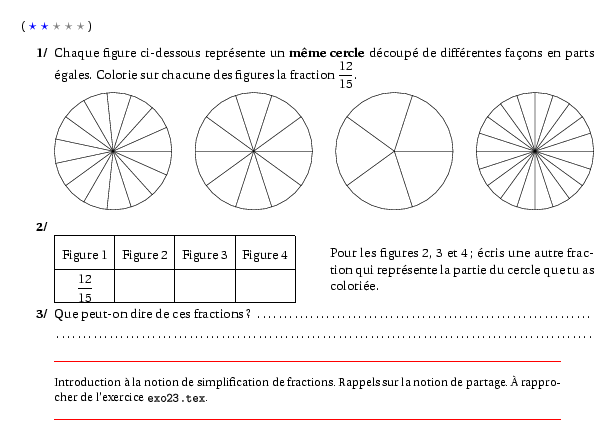
\item Chaque figure ci-dessous représente un {\bf même cercle} découpé
de différentes façons en parts égales. Colorie sur chacune des figures
la fraction $\dfrac{12}{15}$.
\par\includegraphics[scale=.9]{603actiquoeg.9}\hfill\includegraphics[scale=.9]{603actiquoeg.10}\hfill\includegraphics[scale=.9]{603actiquoeg.11}\hfill\includegraphics[scale=.9]{603actiquoeg.12}
\item\subitem{}\par\dispo{1}{
\renewcommand{\arraystretch}{2}
\begin{tabular}{|c|c|c|c|}
\hline
Figure 1&Figure 2&Figure 3&Figure 4\\
\hline
$\dfrac{12}{15}$&&&\\
\hline
\end{tabular}
\renewcommand{\arraystretch}{1}
}{Pour les figures 2, 3 et 4 ; écris une autre fraction qui représente
la partie du cercle que tu as coloriée.}
\item Que peut-on dire de ces fractions ? \dotfill\par\dotfill
\end{myenumerate}
%@Commentaire: Introduction à la notion de simplification de fractions. Rappels sur la notion de partage. \`A rapprocher de l'exercice \verb+exo23.tex+.