%@Titre: Déformons des quadrilatères.
%@metapost:6parallelesexo31.mp
%@Auteur: Galion - Mathématique 4\ieme (1979)\par
\begin{itemize}
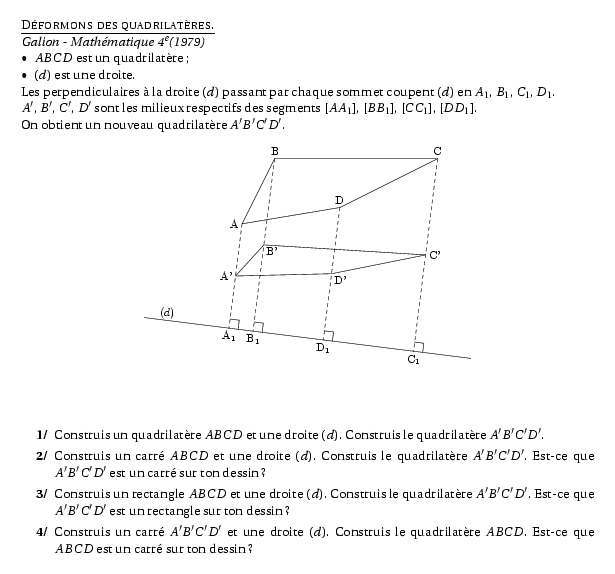
\item[$\bullet$] $ABCD$ est un quadrilatère;
\item[$\bullet$] $(d)$ est une droite.
\end{itemize}
Les perpendiculaires à la droite $(d)$ passant par chaque sommet
coupent $(d)$ en $A_1$, $B_1$, $C_1$, $D_1$.
\par $A'$, $B'$, $C'$, $D'$ sont les milieux respectifs des segments
$[AA_1]$, $[BB_1]$, $[CC_1]$, $[DD_1]$.
\par On obtient un nouveau quadrilatère $A'B'C'D'$.
\[\includegraphics{6parallelesexo31.1}\]
\begin{myenumerate}
  \item Construis un quadrilatère $ABCD$ et une droite
    $(d)$. Construis le quadrilatère $A'B'C'D'$.
  \item Construis un carré $ABCD$ et une droite
    $(d)$. Construis le quadrilatère $A'B'C'D'$. Est-ce que $A'B'C'D'$ est
    un carré sur ton dessin ?
  \item Construis un rectangle $ABCD$ et une droite
    $(d)$. Construis le quadrilatère $A'B'C'D'$. Est-ce que $A'B'C'D'$ est
    un rectangle sur ton dessin ?
  \item Construis un carré $A'B'C'D'$ et une droite
    $(d)$. Construis le quadrilatère $ABCD$. Est-ce que $ABCD$ est
    un carré sur ton dessin ?

\end{myenumerate}