%@Auteur: François Meria\par
\begin{enumerate}[(a)]
    \item
    \begin{multicols}{2}
        \begin{itemize}
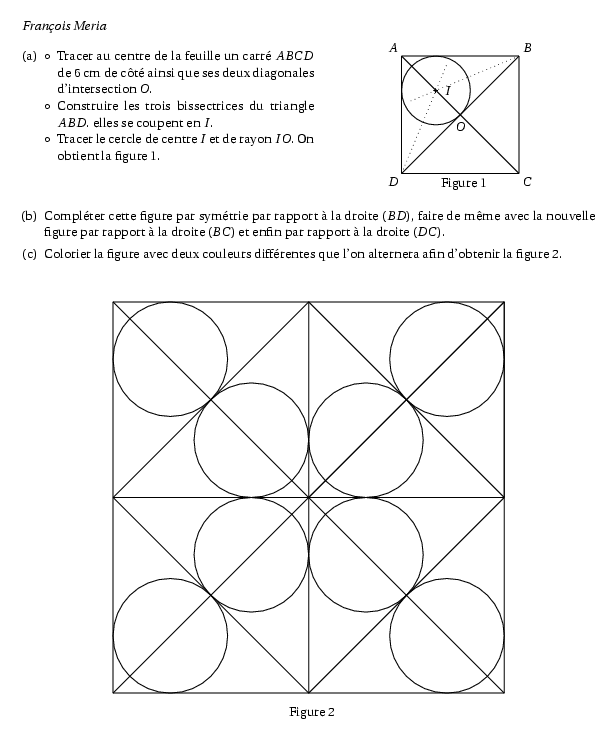
            \item [$\circ$] Tracer au centre de la feuille un carré $ABCD$ de
            $6$~cm de côté ainsi que ses deux diagonales
            d'intersection $O$.
            \item [$\circ$] Construire les trois bissectrices du
            triangle $ABD$. elles se coupent en $I$.
            \item [$\circ$] Tracer le cercle de centre $I$ et de
            rayon $IO$. On obtient la figure 1.
        \end{itemize}
    \begin{center}
    \psset{unit=0.6cm}
        \pspicture(-0.5,-0.5)(6.5,6.5)
            \pstGeonode[PointSymbol=none,PosAngle={225,-45,45,135}](0,0){D}(6,0){C}(6,6){B}(0,6){A}
            \pstLineAB{A}{B}
            \pstLineAB{C}{B}
            \pstLineAB{A}{D}
            \pstLineAB{D}{C}
            \pstLineAB{A}{C}
            \pstLineAB{D}{B}
            \pstInterLL[PointSymbol=none,PosAngle=-90]{D}{B}{A}{C}{O}
            \pstBissectBAC[PointName=none,PointSymbol=none,linestyle=dotted]{A}{B}{D}{M}
            \pstBissectBAC[PointName=none,PointSymbol=none,linestyle=dotted,nodesepB=2.5]{B}{D}{A}{N}
            \pstInterLL[PointSymbol=+]{A}{C}{B}{M}{I}
            \pstCircleOA{I}{O}
            \put(2,-0.7){Figure 1}


        \endpspicture
    \end{center}
    \end{multicols}
    \item Compléter cette figure par symétrie par rapport à la
    droite $(BD)$, faire de même avec la nouvelle figure par
    rapport à la droite $(BC)$ et enfin par rapport à la droite
    $(DC)$.
    \item Colorier la figure avec deux couleurs différentes que l'on alternera afin d'obtenir la figure 2.
\end{enumerate}

\vskip 1cm


\begin{center}
    \psset{unit=1cm}
        \pspicture(0,-6)(12,6) %\psgrid
            \pstGeonode[PointSymbol=none,PointName=none](0,0){D}(6,0){C}(6,6){B}(0,6){A}
            \pstLineAB{A}{B}
            \pstLineAB{C}{B}
            \pstLineAB{A}{D}
            \pstLineAB{D}{C}

            \pstLineAB{A}{C}
            \pstLineAB{D}{B}

            \pstInterLL[PointSymbol=none,PosAngle=-90,PointName=none]{D}{B}{A}{C}{O}
            \pstBissectBAC[PointName=none,PointSymbol=none,linestyle=none]{A}{B}{D}{M}
            \pstBissectBAC[PointName=none,PointSymbol=none,linestyle=none]{B}{D}{A}{N}
            \pstInterLL[PointSymbol=none,PointName=none]{A}{C}{B}{M}{I}
            \pstCircleOA{I}{O}
            \pstOrtSym[PointSymbol=none,PointName=none]{D}{B}{I}{J}
            \pstCircleOA{J}{O}

            \pstOrtSym[PointName=none,PointSymbol=none]{B}{C}{D}{E}
            \pstOrtSym[PointName=none,PointSymbol=none]{B}{C}{A}{F}
            \pstOrtSym[PointName=none,PointSymbol=none]{B}{C}{I}{K}
            \pstOrtSym[PointName=none,PointSymbol=none]{B}{C}{J}{L}
            \pstOrtSym[PointName=none,PointSymbol=none]{B}{C}{O}{O'}
            \pstCircleOA{K}{O'}
            \pstCircleOA{L}{O'}
            \pstLineAB{B}{E}
            \pstLineAB{B}{F}
            \pstLineAB{E}{C}
            \pstLineAB{E}{F}
            \pstLineAB{C}{F}

            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{A}{Z}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{B}{Y}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{F}{X}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{J}{T}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{I}{Q}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{O}{P}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{O'}{S}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{L}{H}
            \pstOrtSym[PointName=none,PointSymbol=none]{D}{C}{K}{H'}

            \pstCircleOA{T}{P}
            \pstCircleOA{H}{S}
            \pstCircleOA{H'}{S}
            \pstCircleOA{Q}{P}

            \pstLineAB{D}{Z}
            \pstLineAB{C}{Y}
            \pstLineAB{E}{X}
            \pstLineAB{E}{F}
            \pstLineAB{C}{F}
            \pstLineAB{C}{X}
            \pstLineAB{Z}{X}
            \pstLineAB{C}{Z}
            \pstLineAB{D}{Y}
            \pstLineAB{Y}{E}
            \put(5.4,-6.7){Figure 2}
        \endpspicture
\end{center}