%@P:exocorcp
%@metapost:airesexos.mp
%@Auteur:Nicolas Roux\par
\begin{myenumerate}
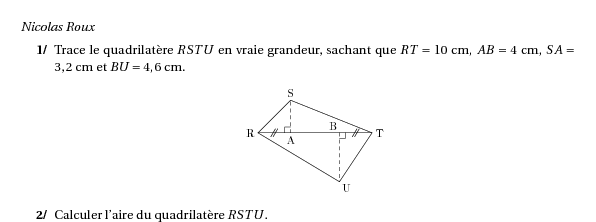
\item Trace le quadrilatère $RSTU$ en vraie grandeur, sachant que $RT=10$~cm, $AB=4$~cm, $SA=3,2$~cm et $BU=4,6$~cm.\\
\[\includegraphics{airesexos.6}\]
\item Calculer l'aire du quadrilatère $RSTU$.
\end{myenumerate}
%@Correction:
\begin{myenumerate}
  \setcounter{enumi}{1}
\item On calcule $RA=(10-4)\div2=3$~cm.
  \begin{multicols}{4}
    \[\Eqalign{
      {\cal A}_{SAR}&=\frac{RA\times SA}2\cr
      {\cal A}_{SAR}&=\frac{3\times3,2}2\cr
      {\cal A}_{SAR}&=4,8~\mbox{cm}^2\cr
    }\]
    \[\Eqalign{
      {\cal A}_{SAT}&=\frac{TA\times SA}2\cr
      {\cal A}_{SAT}&=\frac{7\times3,2}2\cr
      {\cal A}_{SAT}&=11,6~\mbox{cm}^2\cr
    }\]
    \[\Eqalign{
      {\cal A}_{UBR}&=\frac{UB\times BR}2\cr
      {\cal A}_{UBR}&=\frac{4,6\times7}2\cr
      {\cal A}_{UBR}&=16,1~\mbox{cm}^2\cr
    }\]
    \[\Eqalign{
      {\cal A}_{BTU}&=\frac{BT\times BU}2\cr
      {\cal A}_{BTU}&=\frac{3\times4,6}2\cr
      {\cal A}_{BTU}&=6,9~\mbox{cm}^2\cr
    }\]
  \end{multicols}
  Donc l'aire totale est ${\cal A}=4,8+11,6+16,1+6,9=39,4$~cm$^2$.
\end{myenumerate}