Modifié le 30 Octobre 2006 à 16 h 06.
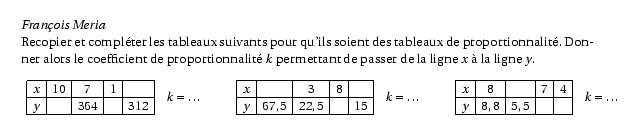
Source
%@Auteur: François Meria\par
Recopier et compléter les tableaux suivants pour qu'ils soient des
tableaux de proportionnalité. Donner alors le coefficient de
proportionnalité $k$ permettant de passer de la ligne $x$ à la
ligne $y$.
\[
\begin{array}{cc}
\begin{array}{|c|c|c|c|c|}
\hline
x & 10 & 7 & 1 & \\
\hline
y & & 364 & & 312 \\
\hline
\end{array}
& k=\ldots\\
\end{array}
\qquad
\begin{array}{cc}
\begin{array}{|c|c|c|c|c|}
\hline
x & & 3 & 8 & \\
\hline
y & 67,5 & 22,5 & & 15 \\
\hline
\end{array}
& k=\ldots\\
\end{array}
\qquad
\begin{array}{cc}
\begin{array}{|c|c|c|c|c|}
\hline
x & 8 & & 7 & 4 \\
\hline
y & 8,8 & 5,5 & & \\
\hline
\end{array}
& k=\ldots\\
\end{array}
\]