%@Auteur: Arnaud Gazagnes\par
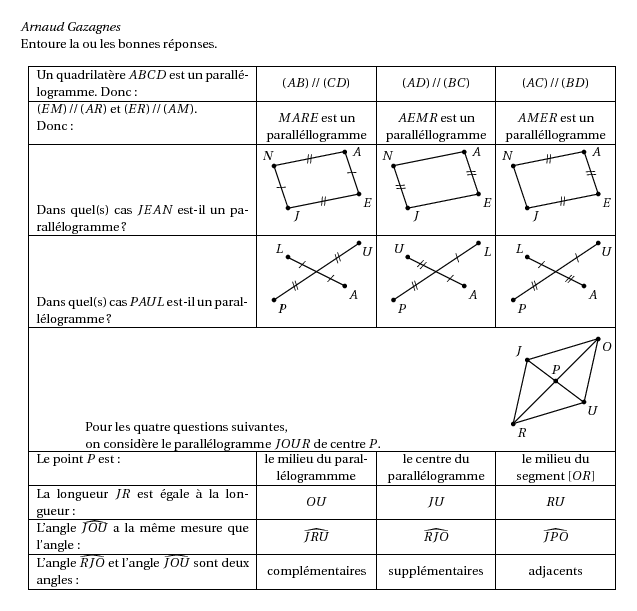
Entoure la ou les bonnes r\'eponses.

\begin{center}
\begin{tabularx}{0.975\textwidth}{|m{6cm}|>{\centering\arraybackslash}X|>{\centering\arraybackslash}X|>{\centering\arraybackslash}X|}
\hline Un quadrilat\`ere $ABCD$ est un parall\'elogramme. Donc :&$(AB)\,/\!/\,(CD)$&$(AD)\,/\!/\,(BC)$&$(AC)\,/\!/\,(BD)$\tabularnewline
\hline $(EM)\,/\!/\,(AR)$ et $(ER)\,/\!/\,(AM)$.\par Donc :&$MARE$ est un parall\'ellogramme&$AEMR$ est un parall\'ellogramme&$AMER$ est un parall\'ellogramme\tabularnewline
\hline Dans quel(s) cas $JEAN$ est-il un parall\'elogramme ?&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-2,-2){J} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,-1){E} 
\pstGeonode[PosAngle=0,PointSymbol=*](2,2){A}
\pstGeonode[PosAngle=120,PointSymbol=*](-3,1){N}
\pstSegmentMark[SegmentSymbol=pstslashh] {J}{E} 
\pstSegmentMark[SegmentSymbol=pstslash] {E}{A} 
\pstSegmentMark[SegmentSymbol=pstslashh] {A}{N} 
\pstSegmentMark[SegmentSymbol=pstslash] {N}{J} 
\end{pspicture}}
&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-2,-2){J} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,-1){E} 
\pstGeonode[PosAngle=0,PointSymbol=*](2,2){A}
\pstGeonode[PosAngle=120,PointSymbol=*](-3,1){N}
\pstLineAB{J}{E} 
\pstSegmentMark[SegmentSymbol=pstslashh] {E}{A} 
\pstLineAB{A}{N} 
\pstSegmentMark[SegmentSymbol=pstslashh] {N}{J} 
\end{pspicture}}
&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-2,-2){J} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,-1){E} 
\pstGeonode[PosAngle=0,PointSymbol=*](2,2){A}
\pstGeonode[PosAngle=120,PointSymbol=*](-3,1){N}
\pstSegmentMark[SegmentSymbol=pstslashh] {J}{E} 
\pstSegmentMark[SegmentSymbol=pstslashh] {E}{A} 
\pstSegmentMark[SegmentSymbol=pstslashh] {A}{N} 
\pstLineAB{N}{J} 
\end{pspicture}}
 \tabularnewline
\hline Dans quel(s) cas $PAUL$ est-il un parall\'elogramme ?&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-3,-2){P} 
\pstGeonode[PosAngle=-45,PointSymbol=*](2,-1){A} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,2){U}
\pstGeonode[PosAngle=135,PointSymbol=*](-2,1){L}
\pstGeonode[PointName=none,PointSymbol=none](0,0){O}
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{P} 
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{U} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{A} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{L} 
\end{pspicture}}
&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-3,-2){P} 
\pstGeonode[PosAngle=-45,PointSymbol=*](2,-1){A} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,2){L}
\pstGeonode[PosAngle=135,PointSymbol=*](-2,1){U}
\pstGeonode[PointName=none,PointSymbol=none](0,0){O}
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{P} 
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{U} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{A} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{L} 
\end{pspicture}}
&
{\psset{unit=0.4cm}\begin{pspicture}(-3.5,-3)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-3,-2){P} 
\pstGeonode[PosAngle=-45,PointSymbol=*](2,-1){A} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,2){U}
\pstGeonode[PosAngle=135,PointSymbol=*](-2,1){L}
\pstGeonode[PointName=none,PointSymbol=none](0,0){O}
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{P} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{L} 
\pstSegmentMark[SegmentSymbol=pstslash] {O}{U} 
\pstSegmentMark[SegmentSymbol=pstslashh] {O}{A} 
\end{pspicture}}
 \tabularnewline
 \hline \multicolumn{3}{|c}{\begin{minipage}{10cm}Pour les quatre questions suivantes,\\ on consid\`ere le parall\'elogramme $JOUR$ de centre $P$.\end{minipage}}& {\psset{xunit=0.4cm,yunit=0.6cm}\begin{pspicture}(-3.5,-2.75)(3.5,2.5) 
\pstGeonode[PosAngle=-45,PointSymbol=*](-3,-2){R} 
\pstGeonode[PosAngle=-45,PointSymbol=*](2,-1){U} 
\pstGeonode[PosAngle=-45,PointSymbol=*](3,2){O}
\pstGeonode[PosAngle=135,PointSymbol=*](-2,1){J}
\pstGeonode[PosAngle=90,PointSymbol=*](0,0){P}
\pstLineAB{J}{O} 
\pstLineAB{O}{U} \pstLineAB{U}{R} \pstLineAB{R}{J} \pstLineAB{J}{U} \pstLineAB{O}{R} \end{pspicture}}\tabularnewline

 \hline Le point $P$ est : & le milieu du parall\'elogrammme&le centre du parall\'elogramme&le milieu du segment $[OR]$\tabularnewline
\hline La longueur $JR$ est \'egale \`a la longueur :&$OU$&$JU$&$RU$ \tabularnewline
\hline L'angle $\widehat{JOU}$ a la m\^eme mesure que l'angle :&$\widehat{JRU}$&$\widehat{RJO}$&$\widehat{JPO}$ \tabularnewline
\hline L'angle $\widehat{RJO}$ et l'angle $\widehat{JOU}$ sont deux angles :&compl\'ementaires&suppl\'ementaires&adjacents \tabularnewline
\hline
\end{tabularx}
\end{center}