%@Auteur: François Meria\par
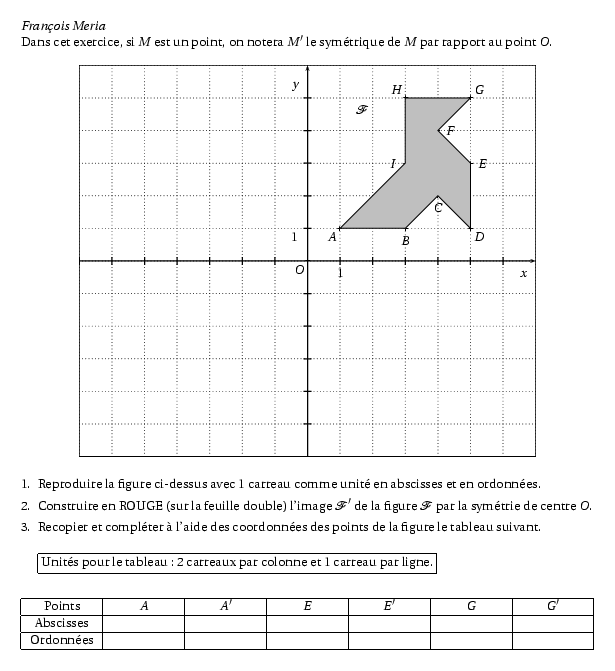
Dans cet exercice, si $M$ est un point, on notera $M'$ le
symétrique de $M$ par rapport au point $O$.

\begin{center}
    \psset{unit=1cm}
    \begin{pspicture*}(-7,-6)(7,6)
        \psframe(-7,-6)(7,6)
        \psgrid[subgriddiv=1,gridlabels=0,griddots=10](-7,-6)(7,6)
        \psaxes[linewidth=1.0pt,labels=none]{->}(0,0)(-7,-6)(7,6)
        \pstGeonode[PointSymbol=+,PosAngle=225](0,0){O}
        \pstGeonode[PointSymbol=+,PosAngle=225](1,1){A}
        \pstGeonode[PointSymbol=+,PosAngle=-90](3,1){B}
        \pstGeonode[PointSymbol=+,PosAngle=-90](4,2){C}
        \pstGeonode[PointSymbol=+,PosAngle=-45](5,1){D}
        \pstGeonode[PointSymbol=+,PosAngle=0](5,3){E}
        \pstGeonode[PointSymbol=+,PosAngle=0](4,4){F}
        \pstGeonode[PointSymbol=+,PosAngle=45](5,5){G}
        \pstGeonode[PointSymbol=+,PosAngle=135](3,5){H}
        \pstGeonode[PointSymbol=+,PosAngle=180](3,3){I}
        \pspolygon[fillstyle=solid,fillcolor=lightgray](A)(B)(C)(D)(E)(F)(G)(H)(I)
        \put(6.5,-0.5){$x$}
        \put(-0.5,5.3){$y$}
        \put(0.9,-0.5){$1$}
        \put(-0.5,0.6){$1$}
        \put(1.5,4.5){$\cal F$}
    \end{pspicture*}
    \end{center}

\begin{enumerate}[1.]
    \item Reproduire la figure ci-dessus avec 1 carreau comme
    unité en abscisses et en ordonnées.
    \item Construire en ROUGE (sur la feuille double) l'image $\cal F'$ de la figure ${\cal F}$ par la symétrie de centre $O$.
    \item Recopier et compléter à l'aide des coordonnées des points de la figure le tableau
    suivant.\\

    \fbox{Unités pour le tableau : 2 carreaux par colonne et 1 carreau
    par ligne.}
\end{enumerate}


\vskip 0.5cm

    \begin{center}
        \begin{tabularx}{\textwidth}{|*{7}{>{\centering}X|}}
        \hline
            Points & $A$ & $A'$ & $E$ & $E'$ & $G$ & $G'$ \tabularnewline
        \hline
            Abscisses & & & & & & \tabularnewline
        \hline
            Ordonnées & & & & & & \tabularnewline
        \hline
        \end{tabularx}
    \end{center}
%\vskip 1.5cm