Modifié le 14 Avril 2007 à 18 h 06.
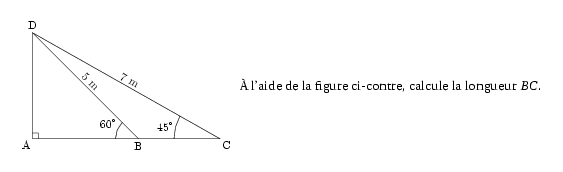
Source
%@P:exocorcp
%@metapost:403ds06.mp
\par\compo{1}{403ds06}{1}{\`A l'aide de la figure ci-contre, calcule la
longueur $BC$.}
%@Correction:
Dans le triangle $ABD$, rectangle en $A$, on a :
\[\Eqalign{
\cos\widehat{ABD}&=\frac{BA}{BD}\cr
\cos60&=\frac{BA}5\cr
BA&=5\times\cos60\cr
BA&=2,5~\mbox{m}\cr
}\]
\setboolean{racine}{true}\pythadroit DAB5{2,5}
\par Dans le triangle $ACD$, rectangle en $A$, le théorème de
Pythagore permet d'écrire :
\[\Eqalign{
DC^2&=DA^2+AC^2\cr
7^2&=18,75+AC^2\cr
49&=18,75+AC^2\cr
49-18,75&=AC^2\cr
30,25&=AC^2\cr
\sqrt{30,25}&=AC^2\cr
5,5&=AC\cr
}\]
Comme $B$ appartient au segment $[AC]$ alors $BC=AC-AB=3$~m.