%@metapost:406ec2.mp
%@Titre:Variations sur un rectangle.
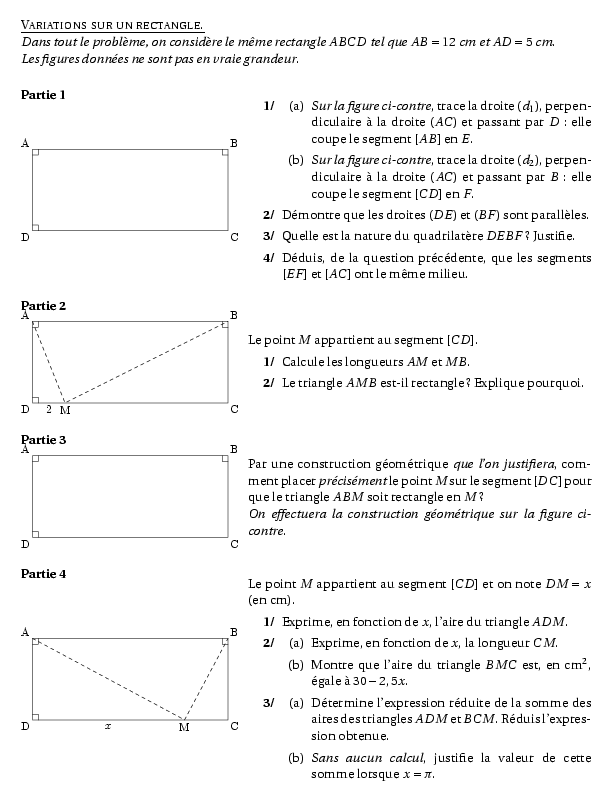
{\em Dans tout le problème, on considère le même rectangle $ABCD$ tel
  que $AB=12$~cm et $AD=5$~cm}.
\\{\em Les figures données ne sont pas en vraie grandeur}.
\paragraph{Partie 1}\hfill\newline
\compo{2}{406ec2}{1}{
  \begin{myenumerate}
    \item
      \begin{enumerate}
      \item {\em Sur la figure ci-contre}, trace la droite $(d_1)$,
        perpendiculaire à la droite $(AC)$ et passant par $D$ : elle
        coupe le segment $[AB]$ en $E$.
      \item {\em Sur la figure ci-contre}, trace la droite $(d_2)$,
        perpendiculaire à la droite $(AC)$ et passant par $B$ : elle
        coupe le segment $[CD]$ en $F$.
      \end{enumerate}
    \item Démontre que les droites $(DE)$ et $(BF)$ sont parallèles.
    \item Quelle est la nature du quadrilatère $DEBF$ ? Justifie.
    \item Déduis, de la question précédente, que les segments $[EF]$
      et $[AC]$ ont le même milieu.
  \end{myenumerate}
}
\paragraph{Partie 2}\hfill\newline
\compo{3}{406ec2}{1}{Le point $M$ appartient au segment $[CD]$.
  \begin{myenumerate}
    \item Calcule les longueurs $AM$ et $MB$.
    \item Le triangle $AMB$ est-il rectangle ? Explique pourquoi.
  \end{myenumerate}
}
\paragraph{Partie 3}\hfill\newline
\compo{4}{406ec2}{1}{
Par une construction géométrique {\em que l'on justifiera}, comment
placer {\em précisément} le point $M$ sur le segment $[DC]$ pour que
le triangle $ABM$ soit rectangle en $M$ ?
\\{\em On effectuera la construction géométrique sur la figure ci-contre}.
}
\paragraph{Partie 4}\hfill\newline
\compo{5}{406ec2}{1}{Le point $M$ appartient au segment $[CD]$ et on
  note $DM=x$ (en cm).
  \begin{myenumerate}
    \item Exprime, en fonction de $x$, l'aire du triangle $ADM$.
    \item
      \begin{enumerate}
      \item Exprime, en fonction de $x$, la longueur $CM$.
      \item Montre que l'aire du triangle $BMC$ est, en cm$^2$, égale
        à $30-2,5x$.
      \end{enumerate}
    \item
      \begin{enumerate}
      \item Détermine l'expression réduite de la somme des aires des
      triangles $ADM$ et $BCM$. Réduis l'expression obtenue.
    \item {\em Sans aucun calcul}, justifie la valeur de cette somme
      lorsque $x=\pi$.
      \end{enumerate}
  \end{myenumerate}
}