Modifié le 26 Octobre 2006 à 14 h 37.
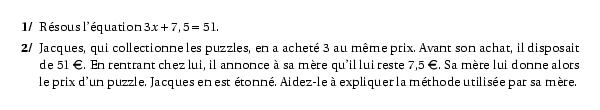
Source
%@P:exocorcp
\begin{myenumerate}
\item Résous l'équation $3x+7,5=51$.
\item Jacques, qui collectionne les puzzles, en a acheté 3 au même prix. Avant son achat, il disposait de 51~\textgreek{\euro}. En rentrant chez lui, il annonce à sa mère qu'il lui reste 7,5~\textgreek{\euro}. Sa mère lui donne alors le prix d'un puzzle. Jacques en est étonné. Aidez-le à expliquer la méthode utilisée par sa mère.
\end{myenumerate}
%@Correction:
\begin{myenumerate}
\item
\[\Eqalign{
\rnode{A}{}&&3x+7,5&=51&&\rnode{B}{}\cr
\rnode{C}{}&&3x+7,5-7,5&=51-7,5&&\rnode{D}{}\cr
\rnode{E}{}&&3x&=43,5&&\rnode{F}{}\cr
\rnode{G}{}&&x&=\frac{43,5}3&&\rnode{H}{}\cr
&&x&=14,5&&\cr
}\]
\ncarc[arcangle=-30]{->}{A}{C}
\nbput{$-7,5$}
\ncarc[arcangle=30]{->}{B}{D}
\naput{$-7,5$}
\ncarc[arcangle=-30]{->}{E}{G}
\nbput{$\div3$}
\ncarc[arcangle=30]{->}{F}{H}
\naput{$\div3$}
\item Elle a posé $x$ le prix d'un puzzle et résolu l'équation $3x+7,5=51$ donc la solution est \[x=14,5\]
\end{myenumerate}