%@metapost:4geoproblemeexo49.mp
%@Auteur:Véronique Glaçon\par
\textbf{\underline{Partie A} :}
\begin{myenumerate}
  \item Où se situe le centre du cercle circonscrit d'un triangle?
  \item Justifie que : \og{\em Dans un triangle équilatéral, le centre
      du cercle circonscrit est aussi le point d'intersection des
      médianes}\fg.
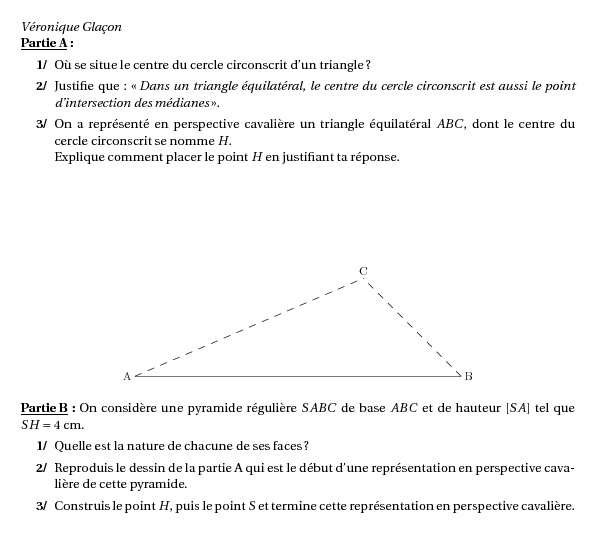
  \item On a représenté en perspective cavalière un triangle
    équilatéral $ABC$, dont le centre du cercle circonscrit se nomme
    $H$.\\Explique comment placer le point $H$ en justifiant ta
    réponse.
\end{myenumerate}
\vspace{2.5cm}
\begin{center}
  \includegraphics{4geoproblemeexo49.1}
\end{center}
\textbf{\underline{Partie B} :} On considère une pyramide régulière $SABC$ de base $ABC$ et de hauteur $[SA]$ tel que $SH=4$~cm.
\begin{myenumerate}
\item Quelle est la nature de chacune de ses faces?
\item Reproduis le dessin de la partie A qui est le début d'une
  représentation en perspective cavalière de cette pyramide.
\item Construis le point $H$, puis le point $S$ et termine cette
  représentation en perspective cavalière.
\end{myenumerate}