%@Auteur: François Meria\par
\begin{multicols}{2}
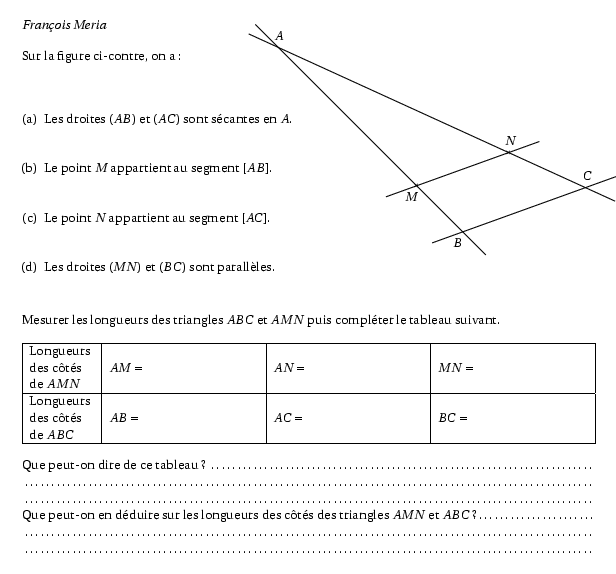
Sur la figure ci-contre, on a :
\begin{enumerate}[(a)]
    \item Les droites $(AB)$ et $(AC)$ sont sécantes en $A$.
    \item Le point $M$ appartient au segment $[AB]$.
    \item Le point $N$ appartient au segment $[AC]$.
    \item Les droites $(MN)$ et $(BC)$ sont parallèles.
\end{enumerate}

\begin{center}
    \psset{unit=1cm}
        \pspicture(0,-2)(8,5) %\psgrid
        \rput{45}{
            \pstGeonode[PointSymbol=none,PosAngle={45,200}](2.5,4.5){A}(2.5,-3.5){B}
            \pstGeonode[PointSymbol=none,PointName=none](6.5,-3.5){T}
            \pstCurvAbsNode[PointSymbol=none,PosAngle=35]{B}{T}{C}{-50}
            \pstHomO[HomCoef=0.75,PointSymbol=+,PosAngle=200]{A}{B}{M}
            \pstHomO[HomCoef=0.75,PointSymbol=+,PosAngle=35]{A}{C}{N}
            \pstLineAB[nodesep=-1]{A}{B}
            \pstLineAB[nodesep=-1]{A}{C}
            \pstLineAB[nodesep=-1]{C}{B}
            \pstLineAB[nodesep=-1]{M}{N}
            }
        \endpspicture
\end{center}
\end{multicols}

\vskip 0.5cm

Mesurer les longueurs des triangles $ABC$ et $AMN$ puis compléter
le tableau suivant.

\begin{center}
\begin{tabularx}{\textwidth}{|c|X|X|X|}
\hline
  \multirow{3}{2cm}{Longueurs des côtés de $AMN$}             &              &              &              \\
 &        $AM=$ &        $AN=$ &        $MN=$ \\
 &              &              &              \\
\hline
\multirow{3}{2cm}{Longueurs des côtés de $ABC$}               &              &              &              \\
 &        $AB=$ &        $AC=$ &        $BC=$ \\
 &              &              &              \\
\hline
\end{tabularx}
\end{center}

Que peut-on dire de ce tableau ? \dotfill\\
\null \dotfill\\
\null \dotfill\\
Que peut-on en déduire sur les longueurs des côtés des triangles
$AMN$ et $ABC$ ?\dotfill\\
\null \dotfill\\
\null \dotfill\\