%@Auteur: François Meria\par
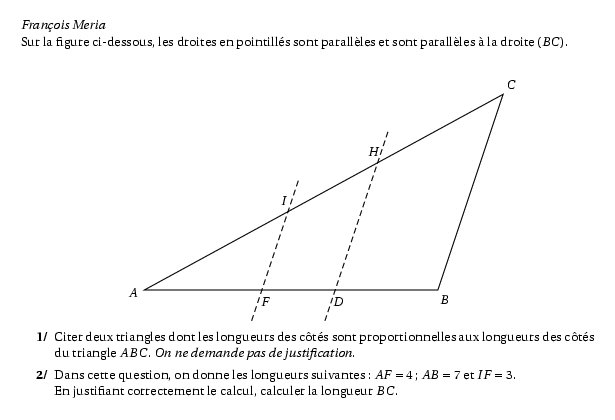
Sur la figure ci-dessous, les droites en pointillés sont
parallèles et sont parallèles à la droite $(BC)$.
\begin{center}
\pspicture(12,7)
    \pstTriangle[PointSymbol=none](1,0){A}(10,0){B}(12,6){C}
    \pstHomO[HomCoef=0.4,PointSymbol=none,PosAngle=-75]{A}{B}{F}
    \pstHomO[HomCoef=0.4,PointSymbol=none,PosAngle=110]{A}{C}{I}
    \pstHomO[HomCoef=0.65,PointSymbol=none,PosAngle=-75]{A}{B}{D}
    \pstHomO[HomCoef=0.65,PointSymbol=none,PosAngle=110]{A}{C}{H}
    \pstLineAB[nodesep=-1,linestyle=dashed]{F}{I}
    \pstLineAB[nodesep=-1,linestyle=dashed]{D}{H}
\endpspicture
\end{center}

\vskip 0.7cm

\begin{myenumerate}
    \item Citer deux triangles dont les longueurs des côtés sont
    proportionnelles aux longueurs des côtés du triangle $ABC$. \textit{On
    ne demande pas de justification}.
    \item Dans cette question, on donne les longueurs suivantes :
    $AF=4$ ; $AB=7$ et $IF=3$.\\
    En justifiant correctement le calcul, calculer la longueur
    $BC$.
\end{myenumerate}