Modifié le 21 Octobre 2006 à 19 h 30.
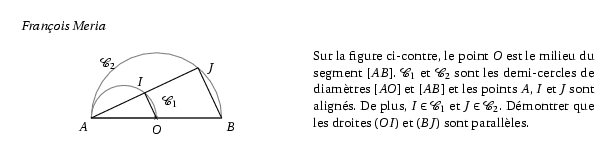
Source
%@Auteur: François Meria\par
\begin{multicols}{2}
\begin{center}
\pspicture(4.3,2.2)
%\psgrid[subgriddiv=2]
\pswedge[linecolor=gray](1,0){1}{0}{180}
\pswedge[linecolor=gray](2,0){2}{0}{180}
\pstGeonode[PointSymbol=none,PosAngle={-135,-45}](0,0){A}(4,0){B}
\pstLineAB{A}{B}
\pstMiddleAB[PointSymbol=x,PosAngle=-90]{A}{B}{O}
\pstCurvAbsNode[PointSymbol=none]{O}{B}{J}{50}
\pstLineAB{A}{J}
\pstLineAB{J}{B}
\pstProjection[PointSymbol=none]{A}{J}{O}{I}
\pstLineAB{O}{I}
% \pstRightAngle[RightAngleSize=0.2]{O}{I}{A}
% \pstRightAngle[RightAngleSize=0.2]{B}{J}{A}
\uput[0]{0}(2,0.5){$\mathcal{C}_1$}
\uput[0]{0}(0.1,1.68){$\mathcal{C}_2$}
\endpspicture
\end{center}
\par\columnbreak\par
Sur la figure ci-contre, le point $O$ est le milieu du segment
$[AB]$. $\mathcal{C}_1$ et $\mathcal{C}_2$ sont les demi-cercles
de diamètres $[AO]$ et $[AB]$ et les points $A$, $I$ et $J$ sont
alignés. De plus, $I\in\mathcal{C}_1$ et $J\in\mathcal{C}_2$.
Démontrer que les droites $(OI)$ et $(BJ)$ sont parallèles.
\end{multicols}