Modifié le 14 Novembre 2007 à 19 h 13.
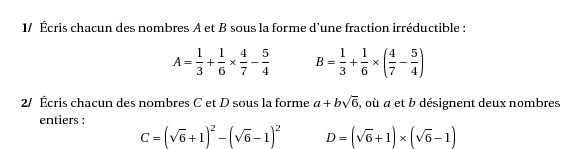
Source
%@P:exocorcp
\begin{myenumerate}
\item \'Ecris chacun des nombres $A$ et $B$ sous la forme d'une
fraction irréductible :
\[\Eqalign{
A&=\frac13+\frac16\times\frac47-\frac54\kern1cm&B&=\frac13+\frac16\times\left(\frac47-\frac54\right)\cr
}\]
\item \'Ecris chacun des nombres $C$ et $D$ sous la forme $a+b\sqrt6$,
où $a$ et $b$ désignent deux nombres entiers :
\[\Eqalign{
C&=\left(\sqrt6+1\right)^2-\left(\sqrt6-1\right)^2\kern1cm&D&=\left(\sqrt6+1\right)\times\left(\sqrt6-1\right)\cr
}\]
\end{myenumerate}
%@Correction:
\[\Eqalign{
A&=\frac13+\frac16\times\frac47-\frac54\kern0.1\linewidth&B&=\frac13+\frac16\times\left(\frac47-\frac54\right)\cr
A&=\frac13+\frac4{42}-\frac54&B&=\frac13+\frac16\times\left(\frac{16}{28}-\frac{35}{28}\right)\cr
A&=\frac{28}{84}+\frac8{84}-\frac{105}{84}&B&=\frac13+\frac16\times\frac{-19}{28}\cr
A&=\frac{-69}{84}&B&=\frac13+\frac{-19}{168}\cr
A&=-\frac{23}{28}&B&=\frac{56}{168}+\frac{-19}{168}\cr
&&B&=\frac{37}{168}\cr
}\]
\[\Eqalign{
C&=\left(\sqrt6+1\right)^2-\left(\sqrt6-1\right)^2\kern0.1\linewidth&D&=\left(\sqrt6+1\right)\times\left(\sqrt6-1\right)\cr
C&=\sqrt6^2+2\sqrt6+1-\left(\sqrt6^2-2\sqrt6+1\right)&D&=\sqrt6^2-1^2\cr
C&=6+2\sqrt6+1-\left(6-2\sqrt6+1\right)&D&=6-1\cr
C&=7+2\sqrt6-\left(7-2\sqrt6\right)&D&=5\cr
C&=7+2\sqrt6-7+2\sqrt6\cr
C&=4\sqrt6\cr
}\]