Modifié le 19 Décembre 2006 à 21 h 20.
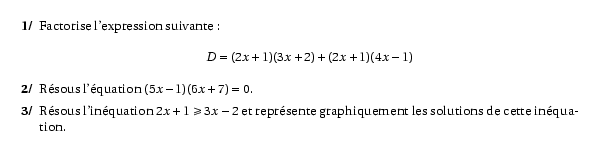
Source
%@metapost:3cumulexo29c.mp
%@P:exocorcp
\begin{myenumerate}
\item Factorise l'expression suivante :
\[D=(2x+1)(3x+2)+(2x+1)(4x-1)\]
\item Résous l'équation $(5x-1)(6x+7)=0$.
\item Résous l'inéquation $2x+1\geqslant3x-2$ et représente
graphiquement les solutions de cette inéquation.
\end{myenumerate}
%@Correction:
\begin{myenumerate}
\item\[\Eqalign{
D&=(2x+1)(3x+2)+(2x+1)(4x-1)\cr
D&=(2x+1)\times\left[(3x+2)+(4x-1)\right]\cr
D&=(2x+1)\times\left[3x+2+4x-1\right]\cr
D&=(2x+1)\times(7x+1)\cr
}\]
\item C'est un produit nul donc
\[\Eqalign{
5x-1&=0&&\mbox{ou}&6x+7&=0\cr
5x&=1&&&6x&=-7\cr
x&=\frac15&&&x&=-\frac76\cr
}\]
Les solutions de cette équation sont $x=\dfrac15$ et $x=-\dfrac76$.
\item\hfill\newline\compo{1}{3cumulexo29c}{1}{\[\Eqalign{
2x+1&\geqslant3x-2\cr
2x-2x+1&\geqslant3x-2x-2\cr
1&\geqslant x-2\cr
1+2&\geqslant x-2+2\cr
3&\geqslant x\cr
}\]
Les solutions sont tous les nombres inférieurs ou égal à 3.}
\end{myenumerate}